Bài 3 trang 64 Toán 11 Tập 2 Chân trời sáng tạo

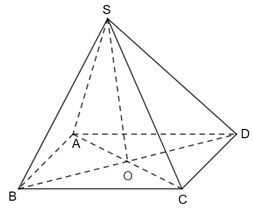
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng , có các cạnh bên đều bằng 2a .

Giải Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng - Chân trời sáng tạo

Bài 3 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng $a \sqrt{2}$ , có các cạnh bên đều bằng 2a .

a) Tính góc giữa SC và AB .

b) Tính diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) .

Lời giải:

Bài 3 trang 64 Toán 11 Tập 2 Chân trời sáng tạo

a) Ta có: AB // CD $\Rightarrow$ (SC, AB) = (SC, CD) = $\hat{SCD}$

Xét ΔSCD , áp dụng định lí cos, ta có :

$\cos \hat{SCD} = \frac{{SC}^{2} + {CD}^{2} - {SD}^{2}}{2 . SC . SD} = \frac{4 a^{2} + 2 a^{2} - 4 a^{2}}{2 .2 a . 2 a} = \frac{1}{4}$

Do đó $\hat{SCD} \approx 75, 5 °$ .

b) Gọi $O = AC \cap BD$

Ta có:

ΔSAC cân tại S nên SO ⊥ AC (1)

ΔSBD cân tại S nên SO ⊥ BD (2)

Từ (1) và (2) suy ra SO ⊥ (ABCD)

Do đó O là hình chiếu vuông góc của S lên (ABCD).

Mà A, B ∈ (ABCD)

Vậy ΔOAB là hình chiếu vuông góc của ΔSAB lên (ABCD).

Ta có: AC = $\sqrt{AB + BC} = \sqrt{2 a^{2} + 2 a^{2}} = 2 a$

Mà ABCD là hình vuông nên O là trung điểm của mỗi đường chéo.

⇒ $AO$ = BO = $\frac{AC}{2} = a$

⇒ $S_{OAB} = \frac{1}{2} . AO . BO = \frac{1}{2} . a . a = \frac{a^{2}}{2}$ .

Vậy diện tích hình chiếu vuông góc của tam giác SAB trên mặt phẳng (ABCD) là $\frac{a^{2}}{2}$ .

Lời giải bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng hay, chi tiết khác: