Thực hành 1 trang 59 Toán 11 Tập 2 Chân trời sáng tạo
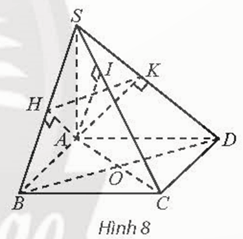
Cho hình chóp S.ABCD có đáy là hình vuông, O là giao điểm của AC và BD, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần luợt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC, SD. Chứng minh rằng:
Giải Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng - Chân trời sáng tạo
Thực hành 1 trang 59 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông, O là giao điểm của AC và BD, SA vuông góc với mặt phẳng (ABCD). Gọi H, I, K lần luợt là hình chiếu vuông góc của điểm A trên các cạnh SB, SC, SD. Chứng minh rằng:
a) CB ⊥ (SAB) và CD ⊥ (SAD) ;
b) HK ⊥ AI .
Lời giải:
a) Ta có: SA ⊥ (ABCD) nên A ⊥ BC
Mà ABCD là hình vuông nên AB ⊥ BC
Và AB ∩ SA = {A}
Do đó BC ⊥ (SAB)
Tương tự: SA ⊥ (ABCD) nên SA ⊥ CD
Mà ABCD là hình vuông nên AD ⊥ CD
Và AD ∩ SA = {A} .
Do đó CD ⊥ (SAD) .
b) Ta có:
Từ (1) và (2) ⇒ SC ⊥ (AHK) ⇒ SC ⊥ HK.(3)
Xét ΔSAB và ΔSAD có:
SA chung
AB = AD
Do đó ΔSAB = ΔSAD (c.g.c)
Suy ra SB = SD; (các cạnh và các góc tương ứng)
Xét tam giác SBD:
SB = SD
⇒ ΔSBD cân tại S.
Xét ΔSAH và ΔSAK có:
; cạnh SA chung ;
Do đó ΔSAH = ΔSAH (cạnh huyền – góc nhọn)
Suy ra SH = SK (các cạnh tương ứng)
Khi ΔSHK cân tại S nên
Ta có:
⇒ (hai góc ở vị trí so le trong)
(4)
Từ (3) và (4) suy ra HK ⊥ (SAC) ⇒ HK ⊥ AI .
Lời giải bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng hay, chi tiết khác: