Bài 5 trang 64 Toán 11 Tập 2 Chân trời sáng tạo

---

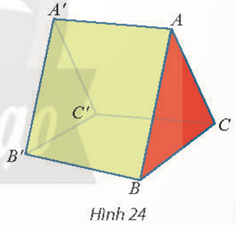
Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m

Giải Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng - Chân trời sáng tạo

Bài 5 trang 64 Toán 11 Tập 2: Một cái lều có dạng hình lăng trụ ABC.A′B′C′ có cạnh bên AA′ vuông góc với đáy (Hình 24). Cho biết AB = AC = 2,4 m; BC = 2 m; AA′ = 3 m

a) Tính góc giữa hai đường thẳng AA′ và BC; A ′B′ và AC.

b) Tính diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB ′CC′ ) .

Lời giải:

a) + Vì AA′ // BB ′ nên (AA′, BC) = (BB′, BC) = $\widehat{B\text{'}\mathrm{BC}}$

Ta có: AA ′ ⊥ (ABC), AA′ // BB ′ ⇒ BB ′ ⊥ (ABC) hay BB ′ ⊥ BC

⇒ $\widehat{B\text{'}\mathrm{BC}}=90°$

+ Vì A′B′ // AB nên (A ′B′, AC) = (AB, AC) = $\widehat{\mathrm{BAC}}$

ΔABC có:

$\cos \widehat{\mathrm{BAC}}=\frac{{\mathrm{AB}}^2+{\mathrm{AC}}^2-{\mathrm{BC}}^2}{2.\mathrm{AB}.\mathrm{AC}}=\frac{5.76+5,76-4}{2.2,4.2,4}=\frac{47}{72}$

⇒ $\widehat{\mathrm{BAC}}\approx 49,2°$

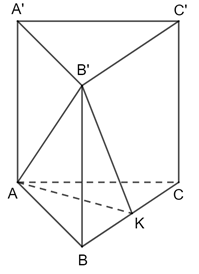
b) Kẻ AK ⊥ BC. Mà AA ′ ⊥ (ABC), AA ′ // BB′

⇒ BB ′ ⊥ (ABC)

⇒ BB ′ ⊥ AK (1)

Ta có: AK ⊥ BC; BC // B′C' ⇒ AK ⊥ B′C′ (2)

Từ (1) và (2) ⇒ AK ⊥ (BB′C′C)

⇒ K là hình chiếu vuông góc của A trên (BB ′ C ′ C)

Mà B, B ′ ∈ (BB ′ C ′ C)

Vậy ΔKBB ′ là hình chiếu vuông góc của ΔABB ′ lên (BB ′C′C ).

Ta có: ΔABC cân tại A có AK ⊥ BC K là trung điểm của BC

⇒ KB = KC = $\frac{\mathrm{BC}}{2}=1$

⇒ $S_{\mathrm{KBB}\text{'}}=\frac{1}{2}.\mathrm{BB}\text{'}.\mathrm{BK}=\frac{3}{2}$ .

Vậy diện tích hình chiếu vuông góc của tam giác ABB′ trên mặt phẳng (BB′CC′ ) là $\frac{3}{2}$ .

Lời giải bài tập Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng hay, chi tiết khác:

• Hoạt động khởi động trang 57 Toán 11 Tập 2: Trong thực tế, người thợ xây dựng thường dùng dây dọi để xác định đường vuông góc với nền nhà ....

• Hoạt động khám phá 1 trang 57 Toán 11 Tập 2: Thả một dây dọi AO chạm sàn nhà tại điểm O. Kẻ một đường thẳng xOy bất kì ....

• Hoạt động khám phá 2 trang 57 Toán 11 Tập 2: Cho đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b trong mặt phẳng (P) ....

• Hoạt động khám phá 3 trang 58 Toán 11 Tập 2: a) Trong không gian, cho điểm O và đường thẳng d. Gọi a, b là hai đường thẳng phân biệt đi qua O và vuông góc ....

• Thực hành 1 trang 59 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông, O là giao điểm của AC và BD, SA vuông góc với mặt phẳng (ABCD) ....

• Vận dụng 1 trang 59 Toán 11 Tập 2: Làm thế nào để dựng cột chống một biển báo vuông góc với mặt đất? ....

• Hoạt động khám phá 4 trang 60 Toán 11 Tập 2: Nêu nhận xét về vị trí tương đối của: a) Hai thân cây cùng mọc vuông góc với mặt đất ....

• Thực hành 2 trang 61 Toán 11 Tập 2: Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA, OB, OC ....

• Thực hành 3 trang 62 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông với AB là cạnh góc vuông và có cạnh SA ....

• Vận dụng 2 trang 62 Toán 11 Tập 2: Một kệ sách có bốn trụ chống và các ngăn làm bằng các tấm gỗ (Hình 18). Làm thế nào ....

• Hoạt động khám phá 5 trang 62 Toán 11 Tập 2: Hai người thợ trong hình đang thả dây dọi từ một điểm M trên trần nhà và đánh dấu điểm M′ ....

• Thực hành 4 trang 63 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Xác định hình chiếu vuông góc ....

• Hoạt động khám phá 6 trang 63 Toán 11 Tập 2: Cho đường thẳng a nằm trong mặt phẳng (P) và b là đường thẳng không thuộc (P) và không vuông góc ....

• Thực hành 5 trang 64 Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc. Vẽ đường thẳng qua O và vuông góc với (ABC) ....

• Vận dụng 3 trang 64 Toán 11 Tập 2: Nêu cách tìm hình chiếu vuông góc của một đoạn thẳng AB trên trần nhà xuống nền nhà bằng hai dây dọi ....

• Bài 1 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD). Cho biết ABCD là hình thang vuông tại A và D, AB = 2AD ....

• Bài 2 trang 64 Toán 11 Tập 2: Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với ....

• Bài 3 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng $a\sqrt{2}$ , có các cạnh bên đều bằng 2a . ....

• Bài 4 trang 64 Toán 11 Tập 2: Cho hình chóp S.ABC có SA = SB = SC = a, $\widehat{\mathrm{ASB}}=90°,$ $\widehat{\mathrm{BSC}}=60°$ và $\widehat{\mathrm{ASC}}=120°$ . Gọi I là trung điểm cạnh AC . Chứng minh SI ⊥ (ABC) . ....