Hoạt động khám phá 2 trang 72 Toán 11 Tập 1 Chân trời sáng tạo
Cho hai hàm số y = f(x) = 2x và y = g(x) = .
Giải Toán 11 Bài 2: Giới hạn của hàm số - Chân trời sáng tạo
Hoạt động khám phá 2 trang 72 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 2x và y = g(x) = .
a) Giả sử (xn) là dãy số bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞. Tìm giới hạn lim[f(xn) + g(xn)].
b) Từ đó, tìm giới hạn , và so sánh với .
Lời giải:
+) Hàm số y = f(x) = 2x xác định trên .
Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:
limf(xn) = lim(2xn) = 2.limxn = 2.1 = 2.
Suy ra = 2.
+) Hàm số y = g(x) = xác định trên ℝ \ {2}.
Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:
limg(xn) =.
Suy ra .
a) Ta có: lim[f(xn) + g(xn)] = limf(xn) + limg(xn) = .
b) Ta có nên .
Ta lại có: .
Vì vậy .
Lời giải bài tập Toán 11 Bài 2: Giới hạn của hàm số hay, chi tiết khác:
Hoạt động khám phá 1 trang 71 Toán 11 Tập 1: Xét hàm số ....
Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau: a) ....
Thực hành 2 trang 73 Toán 11 Tập 1: Tìm các giới hạn sau: a) ....
Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 3 ....
Thực hành 4 trang 76 Toán 11 Tập 1: Tìm các giới hạn sau: a) ....
Vận dụng 1 trang 76 Toán 11 Tập 1: Một cái hồ đang chứa 200m3 nước mặn với nồng độ muối 10kg/m3 ....

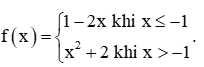 ....
....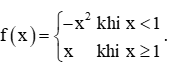 ....
....