Bài 7.3 trang 30 Toán 11 Tập 2 - Kết nối tri thức

Giải Toán 11 Bài 22: Hai đường thẳng vuông góc - Kết nối tri thức

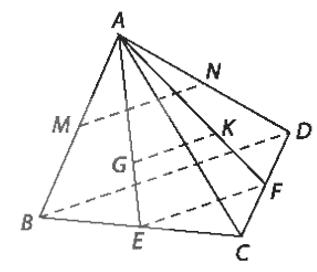
Bài 7.3 trang 30 Toán 11 Tập 2: Cho tứ diện ABCD có $\hat{C B D} = 90 °$ .

a) Gọi M, N tương ứng là trung điểm của AB, AD. Chứng minh rằng MN vuông góc với BC.

b) Gọi G, K tương ứng là trọng tâm của các tam giác ABC, ACD. Chứng minh rằng GK vuông góc với BC.

Lời giải:

Bài 7.3 trang 30 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Xét tam giác ABD, có M là trung điểm của AB, N là trung điểm của AD nên MN là đường trung bình của tam giác ABD, suy ra MN // BD.

Khi đó (MN, BC) = (BD, BC) = $\hat{C B D} = 90 °$ .

Vậy MN vuông góc với BC.

b) Gọi AG cắt BC tại E, suy ra E là trung điểm BC, AK cắt CD tại F, suy ra F là trung điểm CD.

Vì G là trọng tâm tam giác ABC nên $\frac{A G}{A E} = \frac{2}{3}$ , K là trọng tâm tam giác ACD nên $\frac{A K}{A F} = \frac{2}{3}$ .

Xét tam giác AEF có $\frac{A G}{A E} = \frac{A K}{A F} = \frac{2}{3}$ nên GK // EF.

Xét tam giác BCD có E, F lần lượt là trung điểm của BC, CD nên EF là đường trung bình, suy ra EF // BD.

Vì GK // EF và EF // BD nên GK // BD mà BD ⊥ BC nên GK ⊥ BC.

Lời giải bài tập Toán 11 Bài 22: Hai đường thẳng vuông góc hay, chi tiết khác: