Câu 1:
Nếu một quả bóng được thả rơi tự do từ đài quan sát trên sân thượng của tòa nhà Landmark 81 (Thành phố Hồ Chí Minh) cao 461,3 m xuống mặt đất. Có tính được vận tốc của quả bóng khi nó chạm đất hay không? (Bỏ qua sức cản không khí).
Xem lời giải »
Câu 2:
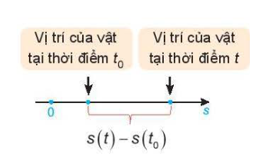
Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).
a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t.
Xem lời giải »
Câu 3:
b) Giới hạn cho ta biết điều gì ?
Xem lời giải »
Câu 4:
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, có dạng Q = Q(t).
a) Tính cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t.
Xem lời giải »
Câu 5:
b) Giới hạn cho ta biết điều gì ?
Xem lời giải »
Câu 6:
Tính đạo hàm của hàm số y = –x2 + 2x + 1 tại điểm x0 = –1.
Xem lời giải »
Câu 7:
Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau:
a) f(x) = c (c là hằng số);
Xem lời giải »
Câu 8:
Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau:
b) f(x) = x.
Xem lời giải »
Câu 9:
Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau:
a) y = x2 + 1
Xem lời giải »
Câu 10:
Tính đạo hàm f'(x0) tại điểm x0 bất kì trong các trường hợp sau:
b) y = kx + c (với k, c là các hằng số).
Xem lời giải »
Câu 11:
Nhận biết tiếp tuyến của đồ thị hàm số
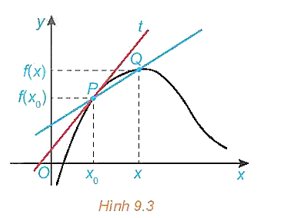
Cho hàm số y = f(x) có đồ thị (C) và P(x0; f(x0)) ∈ (C). Xét điểm Q(x; f(x)) thay đổi trên (C) với x ≠ x0.
a) Đường thẳng đi qua hai điểm P, Q được gọi là một cát tuyến của đồ thị (C) (H.9.3). Tìm hệ số góc kPQ của cát tuyến PQ.
Xem lời giải »
Câu 12:
b) Khi x → x0 thì vị trí của điểm Q(x; f(x)) trên đồ thị (C) thay đổi như thế nào ?
Xem lời giải »
Câu 13:
c) Nếu điểm Q di chuyển trên (C) tới điểm P mà kPQ có giới hạn hữu hạn k thì có nhận xét gì về vị trí giới hạn của cát tuyến QP?
Xem lời giải »
Câu 14:
Tìm hệ số góc của tiếp tuyến của parabol y = x2 tại điểm có hoành độ x0 = .
Xem lời giải »
Câu 15:
Cho hàm số y = x2 có đồ thị là đường parabol (P).
a) Tìm hệ số góc của tiếp tuyến (P) tại điểm có hoành độ x0 = 1.
Xem lời giải »
Câu 17:
Viết phương trình tiếp tuyến của parabol (P): y = –2x2 tại điểm có hoành độ x0 = –1.
Xem lời giải »
Câu 18:
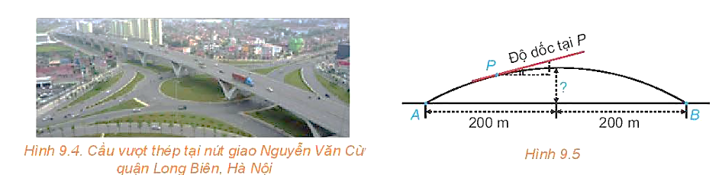
Người ta xây dựng một cây cầu vượt giao thông hình parabol nối hai điểm có khoảng cách là 400 m (H.9.4). Độ dốc của mặt cầu không vượt quá (độ dốc tại một điểm được xác định bởi góc giữa phương tiếp xúc với mặt cầu và phương ngang như Hình 9.5). Tính chiều cao giới hạn từ đỉnh cầu đến mặt đường (làm tròn kết quả đến chữ số thập phân thứ nhất).
Xem lời giải »
Câu 19:
Tính (bằng định nghĩa) đạo hàm của các hàm số sau:
a) y = x2 – x tại x0 = 1;
Xem lời giải »
Câu 20:
Tính (bằng định nghĩa) đạo hàm của các hàm số sau:
b) y = –x3 tại x0 = –1.
Xem lời giải »
Câu 21:
Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
a) y = kx2 + c (với k, c là các hằng số);
Xem lời giải »
Câu 22:
Sử dụng định nghĩa, tính đạo hàm của các hàm số sau:
b) y = x3.
Xem lời giải »
Câu 23:
Viết phương trình tiếp tuyến của parabol y = –x2 + 4x, biết:
a) Tiếp điểm có hoành độ x0 = 1;
Xem lời giải »
Câu 24:
Viết phương trình tiếp tuyến của parabol y = –x2 + 4x, biết:
b) Tiếp điểm có tung độ y0 = 0.
Xem lời giải »
Câu 25:
Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6 m/s thì độ cao h của nó (tính bằng mét) sau t giây được cho bởi công thức h = 19,6t – 4,9t2. Tìm vận tốc của vật khi nó chạm đất.
Xem lời giải »
Câu 26:
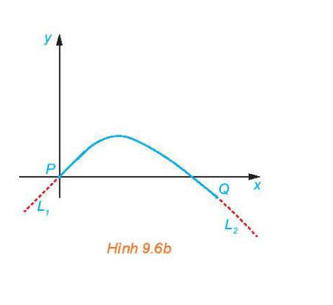
Một kĩ sư thiết kế một đường ray tàu lượn, mà mặt cắt của nó gồm một cung đường cong có dạng parabol (H.9.6a), đoạn dốc lên L1 và đoạn dốc xuống L2 là những phần đường thẳng có hệ số góc lần lượt là 0,5 và –0,75. Để tàu lượn chạy êm và không bị đổi hướng đột ngột, L1 và L2 phải là những tiếp tuyến của cung parabol tại các điểm chuyển tiếp P và Q (H.9.6b). Giả sử gốc tọa độ đặt tại P và phương trình của parabol là y = ax2 + bx + c, trong đó x tính bằng mét.
a) Tìm c.
b) Tính y'(0) và tìm b.
Xem lời giải »
Câu 27:
c) Giả sử khoảng cách theo phương ngang giữa P và Q là 40 m. Tìm a.
d) Tìm chênh lệch độ cao giữa hai điểm chuyển tiếp P và Q.
Xem lời giải »