Phép chiếu song song (Lý thuyết Toán lớp 11) | Kết nối tri thức
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 14: Phép chiếu song song sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.
Phép chiếu song song (Lý thuyết Toán lớp 11) | Kết nối tri thức
Lý thuyết Phép chiếu song song
1. Phép chiếu song song
Cho mặt phẳng (α) và đường thẳng ∆ cắt (α). Với mỗi điểm M trong không gian ta xác định điểm M’ như sau:
- Nếu M thuộc ∆ thì M' là giao điểm của (α) và ∆.
- Nếu M không thuộc ∆ thì M' là giao điểm của (α) và đường thẳng qua M song song với ∆.
Điểm M' được gọi là hình chiếu song song của điểm M trên mặt phẳng (α) theo phương ∆.
Phép đặt tương ứng với mỗi điểm M với hình chiếu M' của nó được gọi là phép chiếu song song lên (α) theo phương ∆.
Mặt phẳng (α) được gọi là mặt phẳng chiếu, phương ∆ được gọi là phương chiếu.
- Cho hình ℋ, tập hợp ℋ ' các hình chiếu M' của các điểm M thuộc ℋ qua phép chiếu song song được gọi là hình chiếu của ℋ qua phép chiếu song song đó.
Chú ý: Nếu một đường thẳng song song với phương chiếu thì hình chiếu của đường thẳng đó là một điểm. Kể từ đây, nếu không nói gì thêm ta chỉ xét các phép chiếu mà phương chiếu không song song với mặt phẳng chiếu.
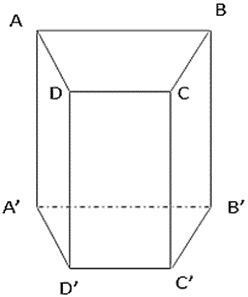
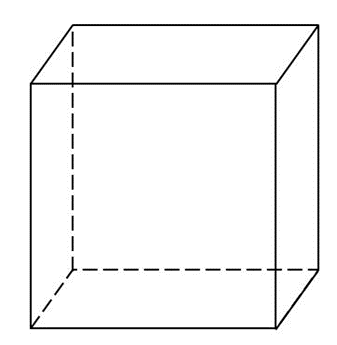
Ví dụ: Cho hình lăng trụ tứ giác ABCD.A'B'C'D'. Xác định hình chiếu của điểm A trên mặt phẳng (A'B'C'D') theo phương CC'.
Hướng dẫn giải
Vì ABCD.A'B'C'D' là hình lăng trụ nên AA' // BB' // CC' // DD'.
Vì A' thuộc mặt phẳng (A'B'C'D') nên A' là hình chiếu của A trên mặt phẳng (A'B'C'D') theo phương CC’.
2. Tính chất của phép chiếu song song
- Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó. Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
- Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
- Phép chiếu song song giữ nguyên tỉ số độ dài của hai đoạn thẳng cùng nằm trên một đường thẳng hoặc nằm trên hai đường thẳng song song.
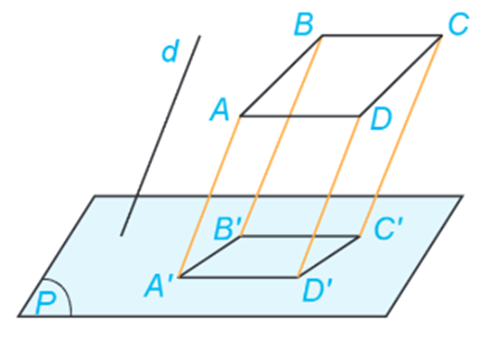
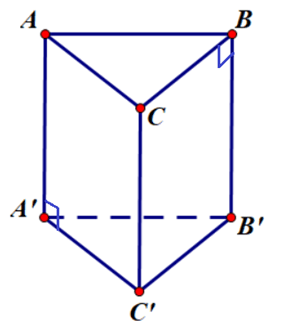
Ví dụ: Cho hình bình hành ABCD và gọi A'B'C'D' là hình chiếu của ABCD trên mặt phẳng (P) theo phương d như hình vẽ dưới. Chứng minh rằng tứ giác A'B'C'D' là hình bình hành.
Hướng dẫn giải
Vì ABCD là hình bình hành nên AB // CD, do đó hình chiếu của AB là A'B' song song với hình chiếu của CD là C'D'. Tương tự A'D' // B'C'.
Tứ giác A'B'C'D' có A'B' // C'D' và A'D' // B'C' nên nó là hình bình hành.
3. Hình biểu diễn của một hình không gian
- Hình biểu diễn của một hình trong không gian là hình chiếu song song của hình đó trên một mặt phẳng theo một phương chiếu nào đó hoặc hình đồng dạng với hình chiếu đó.
Khi hình phẳng nằm trong mặt phẳng không song song với phương chiếu thì hình biểu diễn của hình phẳng đó có các tính chất sau:
+ Hình biểu diễn của một tam giác (cân, đều, vuông) là một tam giác;
+ Hình biểu diễn của hình vuông, hình chữ nhật, hình thoi, hình bình hành là hình bình hành;
+ Hình biểu diễn của hình thang ABCD với AB // CD là một hình thang A'B'C'D' với A'B' // C'D' thỏa mãn .
+ Hình biểu diễn của hình tròn là hình elip.
Ví dụ:
- Hình lập phương
- Hình lăng trụ
Bài tập Phép chiếu song song
Bài 1: Những mệnh đề nào trong các mệnh đề sau đây là đúng?
a) Hình thang là hình biểu diễn của hình bình hành.
b) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng cắt nhau.
c) Phép chiếu song song biến tam giác cân thành tam giác đều.
Hướng dẫn giải
a) Sai. Vì hai cạnh bên của hình thang không song song trong khi đó cặp cạnh đối của hình bình hành thì song song.
b) Sai. Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
c) Sai. Vì phép chiếu song song biến tam giác cân thành tam giác.
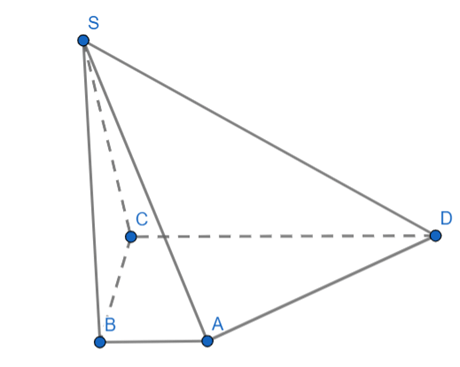
Bài 2: Vẽ hình biểu diễn của hình chóp S.ABCD có đáy ABCD là hình thang, AB song song với CD và AB = 3 cm, CD = 9 cm.
Hướng dẫn giải
Hình chóp S.ABCD có các mặt bên là hình tam giác nên hình biểu diễn các mặt bên là hình tam giác.
Hình thang ABCD có AB // CD và AB = 3 cm, CD = 9 cm nên hình biểu diễn của ABCD là một hình thang có đáy CD gấp ba lần đáy AB và hai đáy này song song với nhau.
Từ đó, ta vẽ được hình biểu diễn của S.ABCD như hình dưới đây.
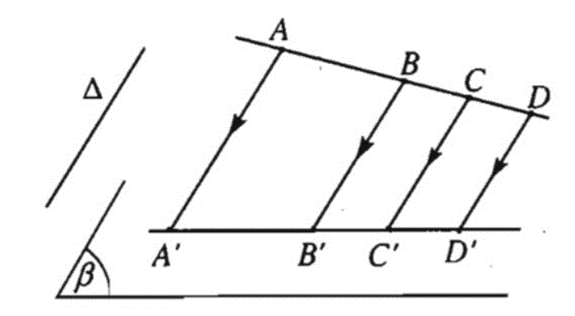
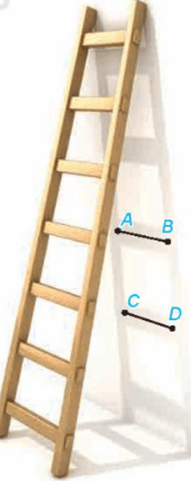
Bài 3: Trong hình bên, AB và CD là bóng của hai thanh chắn của một chiếc thang dưới ánh mặt trời. Hãy giải thích tại sao AB song song với CD.
Hướng dẫn giải
Vì các thanh chắn của chiếc thang song song với nhau, theo tính chất của phép chiếu song song, thì hình chiếu của các thanh chắn cũng song song với nhau.
AB, CD là hình chiếu của hai thanh chắn do đó AB // CD.
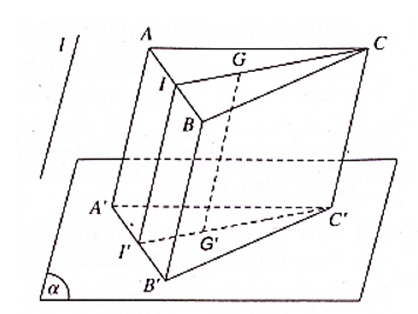
Bài 4: Chứng minh rằng trọng tâm G của tam giác ABC có hình chiếu song song là trọng tâm G' của tam giác A'B'C' trong đó A'B'C' là hình chiếu song song của tam giác ABC.
Hướng dẫn giải
Gọi I là trung điểm của cạnh AB.
Ta có: A, I, B thẳng hàng và AI = IB
Do vậy A', I', B' thẳng hàng và A'I' = I'B', tức I' là trung điểm B'A'
Hay hình chiếu I' của I là trung điểm của A'B'.
Vì G là trọng tâm của tam giác ABC nên C, G, I thẳng hàng
Do G ∈ CI nên G' ∈ C'I';
Vậy G' là trọng tâm tam giác A'B'C'.
Học tốt Phép chiếu song song
Các bài học để học tốt Phép chiếu song song Toán lớp 11 hay khác: