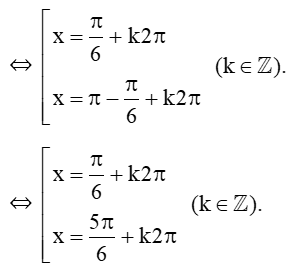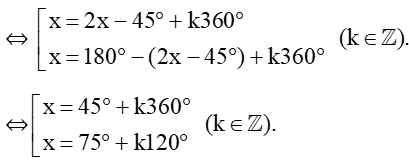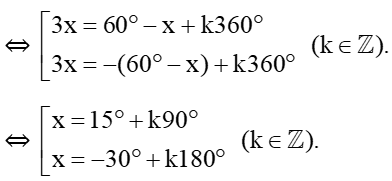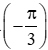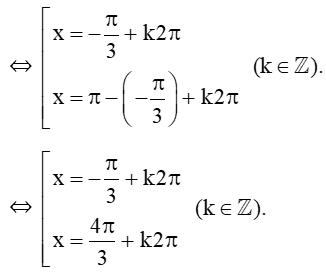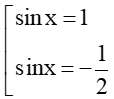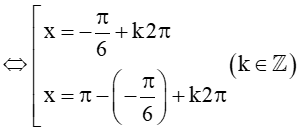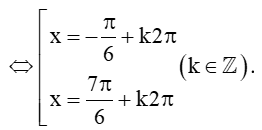Phương trình lượng giác cơ bản (Lý thuyết Toán lớp 11) | Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 4: Phương trình lượng giác cơ bản sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.

Phương trình lượng giác cơ bản (Lý thuyết Toán lớp 11) | Kết nối tri thức

Lý thuyết Phương trình lượng giác cơ bản

1. Khái niệm phương trình tương đương

- Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.

- Nếu phương trình f(x) = 0 tương đương với phương trình g(x) = 0 thì ta viết f(x) = 0 ⇔ g(x) = 0.

Chú ý:

- Hai phương trình vô nghiệm là tương đương.

- Để giải phương trình, thông thường ta biến đổi phương trình đó thành một phương trình tương đương đơn giản hơn. Các phép biến đổi như vậy gọi là các phép biến đổi tương đương.

Nếu thực hiện các phép biến đổi sau đây trên một phương trình mà không làm thay đổi điều kiện của nó thì ta được một phương trình mới tương đương với phương trình đã cho:

a) Cộng hay trừ hai vế với cùng một số hoặc một biểu thức:

f(x) = g(x) ⇔ f(x) + h(x) = g(x) + h(x).

b) Nhân hoặc chia hai vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0:

f(x) = g(x) ⇔ f(x)h(x) = g(x)h(x), (h(x) ≠ 0).

Ví dụ: Phương trình –4x + 4 = 0 có tương đương với phương trình x² – 2x + 1 = 0 hay không ?

Hướng dẫn giải

Tập nghiệm của phương trình –4x + 4 = 0 là S₁ = {1}

Tập nghiệm của phương trình x² – 2x + 1 = 0 là S₂ = {1}

Suy ra S₁ = S₂.

Vậy hai phương trình đã cho tương đương.

2. Phương trình sinx = m

- Phương trình sinx = m có nghiệm khi và chỉ khi |m| ≤ 1;

- Khi |m| ≤ 1 sẽ tồn tại duy nhất 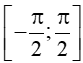$\alpha \in$ thỏa mãn sinα = m. Khi đó

sin x = m ⇔ sin x = sinα ⇔ 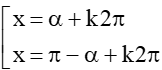(k$\in$Z)

Chú ý:

a) Nếu số đo của góc α được cho bằng đơn vị độ thì

sin x = sin α° ⇔ 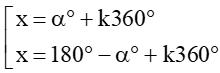(k$\in$Z)

b) Một số trường hợp đặc biệt

+) sin x = 0 ⇔ x = kℼ, k ∈ ℤ.

+) sin x = 1 ⇔ $x=\frac{\pi }{2}+k2\pi$, k ∈ ℤ.

+ sin x = –1 ⇔ $x=-\frac{\pi }{2}+k2\pi$, k ∈ ℤ.

c) sin u = sin v ⇔ 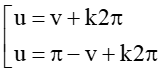(k ∈ ℤ).

Ví dụ: Giải các phương trình sau:

a) sin x = $\frac{1}{2}$ ;

b) sinx = sin (2x – 45°).

Hướng dẫn giải

a) sin x = $\frac{1}{2}$ ⇔ sinx = sin$\frac{\pi }{6}$

b) sinx = sin (2x – 45°)

3. Phương trình cosx = m

- Phương trình cosx = m có nghiệm khi và chỉ khi |m| ≤ 1;

- Khi |m| ≤ 1 sẽ tồn tại duy nhất α ∈ [0; ℼ] thỏa mãn cosα = m. Khi đó

cos x = m ⇔ cosx = cosα ⇔ 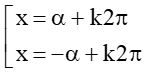(k ∈ ℤ).

Chú ý:

a) Nếu số đo của góc α được cho bằng đơn vị độ thì

cos x = cos α° ⇔ 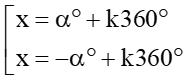(k ∈ ℤ).

b) Một số trường hợp đặc biệt

+) cos x = 0 ⇔ $x=\frac{\pi }{2}+k\pi$, k ∈ ℤ.

+) cos x = 1 ⇔ x = k2ℼ, k ∈ ℤ.

+) cos x = –1 ⇔ x = ℼ + k2ℼ, k ∈ ℤ.

c) cos u = cos v ⇔ u = ±v + k2ℼ (k ∈ ℤ).

Ví dụ: Giải phương trình sau:

a) cosx = $\frac{1}{2}$ ;

b) cos 3x = cos (60° – x).

Hướng dẫn giải

a) cos x = $\frac{1}{2}$ ⇔ cosx = cos$\frac{\pi }{3}$⇔ (k ∈ ℤ).

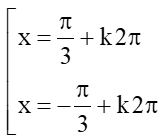
b) cos3x = cos (60° – x)

⇔ 3x = ± (60° – x) + k360° (k ∈ ℤ).

4. Phương trình tan x = m

- Phương trình tan x = m có nghiệm với mọi m.

- Với mọi m ∈ ℝ, tồn tại duy nhất 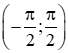$\alpha \in$ thỏa mãn tan α = m. Khi đó

tan x = m ⇔ tanx = tan α ⇔ x = α + kℼ (k ∈ ℤ).

Chú ý: Nếu số đo của góc α được cho bằng đơn vị độ thì

tanx = tan α° ⇔ x = α° + k180° (k ∈ ℤ).

Ví dụ: Giải phương trình tan x = $\frac{\sqrt{3}}{3}$.

Hướng dẫn giải

tan x = $\frac{\sqrt{3}}{3}$⇔ tan x = tan$\frac{\pi }{6}$ ⇔ x = $\frac{\pi }{6}$+k$\pi$, (k ∈ ℤ).

5. Phương trình cot x = m

- Phương trình cot x = m có nghiệm với mọi m.

- Với mọi m ∈ ℝ, tồn tại duy nhất α ∈ (0; ℼ) thỏa mãn cot α = m. Khi đó

cot x = m ⇔ cotx = cot α ⇔ x = α + kℼ (k ∈ ℤ).

Chú ý: Nếu số đo của góc α được cho bằng đơn vị độ thì

cot x = cot α° ⇔ x = α° + k180° (k ∈ ℤ).

Ví dụ: Giải phương trình cot x = $\frac{\sqrt{3}}{3}$ .

Hướng dẫn giải

cot x = $\frac{\sqrt{3}}{3}$⇔ cot x = cot$\frac{\pi }{3}$ ⇔ x = $\frac{\pi }{3}$+k$\pi$ , (k ∈ ℤ).

6. Sử dụng máy tính cầm tay tìm một góc khi biết giá trị lượng giác của nó

Để tìm số đo ta thực hiện các bước sau:

Bước 1: Chọn đơn vị đo góc (độ hoặc rađian).

Muốn tìm số đo độ (dòng trên cùng của màn hình xuất hiện chữ nhỏ D), ta ấn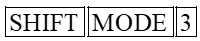

Muốn tìm số đo rađian (dòng trên cùng của màn hình xuất hiện chữ nhỏ R), ta ấn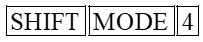

Bước 2: Tìm số đo góc

Khi biết sin, côsin hay tang của góc α cần tìm bằng m, ta lần lượt ấn các phím và một trong các phím và , rồi nhập giá trị lượng giác m và cuối cùng ấn phím . Lúc này trên màn hình cho kết quả là số đo của góc α (độ hoặc rađian).

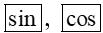
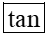
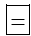
Chú ý:

- Khi ở chế độ rađian, các phím (sin^–1), (tan^–1), cho ta kết quả là một số thuộc khoảng 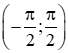, phím (cos^–1) cho kết quả là một số thuộc khoảng (0; ℼ), tất nhiên với (sin^–1), (cos^–1) thì |m| ≤ 1.

- Khi ở chế độ số đo độ, các phím (sin^–1) và (tan^–1) cho kết quả là số đo góc α từ –90° đến 90°, phím (cos^–1) cho kết quả là số đo góc α từ 0° đến 180°, với (sin^–1) và (cos^–1) thì |m| ≤ 1.

- Khi có kết quả (trường hợp chọn đơn vị đo độ), ấn phím thì đưa kết quả về dạng độ – phút – giây.

Ví dụ: Sử dụng máy tính cầm tay, tìm số đo độ và rađian của góc α, biết sinα = 0,45.

Hướng dẫn giải

Số đo độ:

sinα	Bấm phím	Màn hình hiện	Kết quả của α (số gần đúng)
0,45		26°44’37.26’’	26°44’37’’

Vậy α ≈ 26°44’37’’.

Số đo rađian

sinα	Bấm phím	Màn hình hiện	Kết quả của α (số gần đúng)
0,45		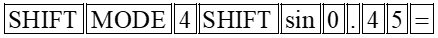0.466765339	0,46677

Vậy α ≈ 0,46677 rad.

Bài tập Phương trình lượng giác cơ bản

Bài 1. Giải các phương trình sau:

a) sin x = $-\frac{\sqrt{3}}{2}$ ;

b) cot (2x – 3) = cot$\frac{\pi }{7}$ .

Hướng dẫn giải

a) sin x = $-\frac{\sqrt{3}}{2}$

⇔ sinx = sin

b) cot (2x – 3) = cot$\frac{\pi }{7}$

⇔ 2x – 3 = $\frac{\pi }{7}$+k$\pi$

⇔ x = $\frac{\pi +21}{14}+k\frac{\pi }{2}$ (k ∈ ℤ).

Bài 2. Giải các phương trình sau:

a) sin x + cos 2x = 0;

b) cos2x = – cos 5x.

Hướng dẫn giải

a) Ta có sin x + cos 2x = 0

⇔ sin x + 1 – 2sin² x = 0

⇔ – 2sin² x + sin x + 1 = 0

⇔

+ Với sin x = 1 ta có: sinx = 1 ⇔ $x=\frac{\pi }{2}+k2\pi ,\text{(k}\in \mathbb{Z}\text{).}$

+ Với sin x = $-\frac{1}{2}$ , ta có: sin x = $-\frac{1}{2}$

Vậy $x=-\frac{\pi }{6}+k2\pi ,x=\frac{7\pi }{6}+k2\pi ,x=\frac{\pi }{2}+k2\pi ,\text{(k}\in \mathbb{Z}\text{).}$

b) Ta có cos2x = – cos 5x ⇔ cos2x = cos$\left(\pi -5x\right)$

Học tốt Phương trình lượng giác cơ bản

Các bài học để học tốt Phương trình lượng giác cơ bản Toán lớp 11 hay khác:

• Giải sgk Toán 11 Bài 4: Phương trình lượng giác cơ bản