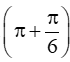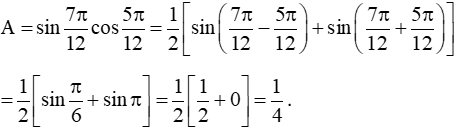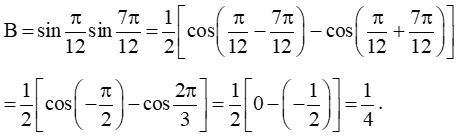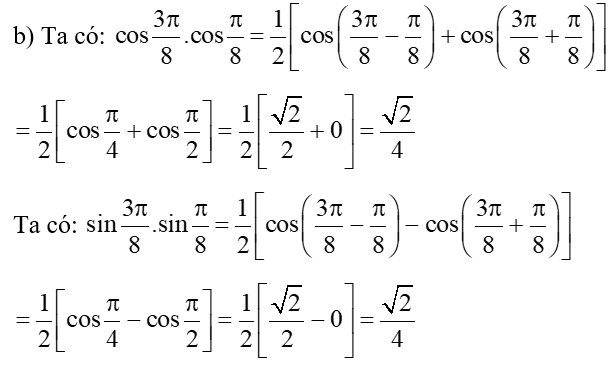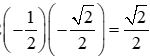Công thức lượng giác (Lý thuyết Toán lớp 11) | Kết nối tri thức
Haylamdo biên soạn và sưu tầm với tóm tắt lý thuyết Toán 11 Bài 2: Công thức lượng giác sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 11 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 11.
Công thức lượng giác (Lý thuyết Toán lớp 11) | Kết nối tri thức
Lý thuyết Công thức lượng giác
1. Công thức cộng
cos (a – b) = cosa cosb + sina sinb
cos (a + b) = cosa cosb – sina sinb
sin (a – b) = sina cosb – cosa sinb
sin (a + b) = sina cosb + cosa sinb
tan (a-b) =
tan (a+b) =
(giả thiết các biểu thức đều có nghĩa).
Ví dụ: Không dùng máy tính, hãy tính sin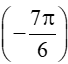
Hướng dẫn giải
Ta có
sin 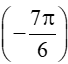
= -sincos - cossin = -0. - (-1). = .
Ta có
tan15o = tan(60o - 45o) =
2. Công thức nhân đôi
sin2a = 2sina cosa
cos2a = cos2a – sin2a = 2cos2 – 1 = 1 – 2sin2a
tan2a = .
Chú ý: Từ công thức nhân đôi suy ra công thức hạ bậc:
.
Ví dụ: Biết sinα = và 0 < α < . Tính sin2α ; cos2α và tan2α.
Hướng dẫn giải
Vì 0 < α < nên cosα > 0.
Ta có:
sin2α + cos2α = 1 ⇒ cos2α = 1 – sin2α = 1-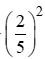
⇒ cosα = .
Ta có: sin2α = 2sinα cosα =
cos2α = 1 – 2sin2α = 1 - 2.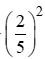
⇒ tan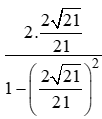
3. Công thức biến đổi tích thành tổng
cosacosb = [cos(a-b) + cos(a+b)]
sinasinb = [cos(a-b) - cos(a+b)]
sinacosb = [sin(a-b) + sin(a+b)].
Ví dụ: Tính giá trị của biểu thức
a) A = ;
b) B = .
Hướng dẫn giải
a) Ta có:
Vậy A = .
b) Ta có:
Vậy B = .
4. Công thức biến đổi tổng thành tích
cosu + cosv = 2coscos
cosu - cosv = -2sinsin
sinu + sinv = 2sincos
sinu - sinv = 2cossin.
Ví dụ: ChoA = cos.cos và B = cos + cos. Không dùng máy tính, tính giá trị của biểu thức .
Hướng dẫn giải
Ta có:
B = cos + cos = 2.cos.cos
= 2.cos.cos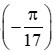
Suy ra .
Bài tập Công thức lượng giác
Bài 1. Tính sin2a và tan2a biết cos a = và <a<2.
Hướng dẫn giải
Vì <a<2nên sina < 0.
Ta có:
sin2a + cos2a = 1 ⇒ sin2a = 1 – cos2a = 1 - 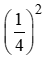
⇒ sina = .
Ta có: sin2a = 2sina cosa = 2.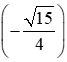
Ta có: tana =
⇒=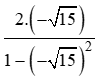
Bài 2. Tính
a) sin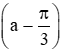
b) cos.cos + sin.sin.
Hướng dẫn giải
a) Vì 0<a< nên cosa > 0.
Ta có: sin2a + cos2a = 1 ⇒ cos2a = 1 – sin2a = 1-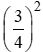
⇒ cosa = .
Vậy sin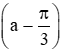
Suy ra: .
Bài 3. Tính
a) cos(–15°) + cos255°;
b) sinsin.
Hướng dẫn giải
a) Ta có:
cos(-15o) + cos255o = 2.cos.cos
= 2.cos120o.cos(135o) = 2
Vậy cos(–15°) + cos255° = .
b) Ta có:
Vậy .
Học tốt Công thức lượng giác
Các bài học để học tốt Công thức lượng giác Toán lớp 11 hay khác: