Giải Toán 11 trang 109 Tập 2 Kết nối tri thức

❮ Bài trước Bài sau ❯

Với Giải Toán 11 trang 109 Tập 2 trong Bài tập ôn tập cuối năm Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 109.

Giải Toán 11 trang 109 Tập 2 Kết nối tri thức

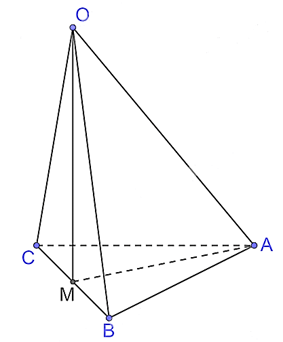
Bài 31 trang 109 Toán 11 Tập 2: Cho tứ diện OABC có OA = OB = OC = a, $\hat{A O B} = \hat{A O C} = 60 °$ và $\hat{B O C} = 90 °$ .

a) Chứng minh rằng (OBC) $⊥$ (ABC).

b) Tính theo a khoảng cách từ O đến mặt phẳng (ABC) và thể tích khối tứ diện OABC.

Lời giải:

Bài 31 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Gọi M là trung điểm của BC.

Xét tam giác OBC có OB = OC = a nên tam giác OBC cân tại O mà OM là trung tuyến nên OM đồng thời là đường cao hay OM $⊥$ BC.

Vì tam giác OAC có OA = OC = a và $\hat{A O C} = 60 °$ nên tam giác OAC đều, suy ra AC = a.

Vì tam giác OAB có OA = OB = a và $\hat{A O B} = 60 °$ nên tam giác OAB đều, suy ra AB = a.

Xét tam giác OBC vuông tại O, có BC = $\sqrt{O C^{2} + O B^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .

Xét tam giác OBC vuông tại O, OM là đường cao, có

$\frac{1}{O M^{2}} = \frac{1}{O B^{2}} + \frac{1}{O C^{2}}$ $= \frac{1}{a^{2}} + \frac{1}{a^{2}} = \frac{2}{a^{2}}$ $\Rightarrow O M = \frac{a}{\sqrt{2}}$ .

Vì BC² = 2a² = a² + a² = AB² + AC² nên tam giác ABC vuông tại A.

Mặt khác AB = AC nên tam giác ABC cân tại A có AM là trung tuyến nên AM đồng thời là đường cao hay AM $⊥$ BC.

Xét tam giác ABC vuông tại A, AM là đường cao có:

$\frac{1}{A M^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}}$ $= \frac{1}{a^{2}} + \frac{1}{a^{2}} = \frac{2}{a^{2}}$ $\Rightarrow A M = \frac{a}{\sqrt{2}}$ .

Vì OA² = a² = $\frac{a^{2}}{2} + \frac{a^{2}}{2}$ = OM² + AM² nên tam giác OMA vuông tại M, suy ra OM ^ MA.

Vì OM $⊥$ MA và OM $⊥$ BC nên OM $⊥$ (ABC) mà OM $\subset$ (OBC), suy ra (OBC) $⊥$ (ABC).

b) Vì OM $⊥$ (ABC) nên d(O, (ABC)) = OM = $\frac{a}{\sqrt{2}}$ .

Có $S_{A B C} = \frac{1}{2} \cdot A B \cdot A C = \frac{a^{2}}{2}$ . Khi đó $V_{O A B C} = \frac{1}{3} \cdot S_{A B C} \cdot O M$ $= \frac{1}{3} \cdot \frac{a^{2}}{2} \cdot \frac{a}{\sqrt{2}} = \frac{a^{3} \sqrt{2}}{12}$ .

Vậy $V_{O A B C} = \frac{a^{3} \sqrt{2}}{12}$ .

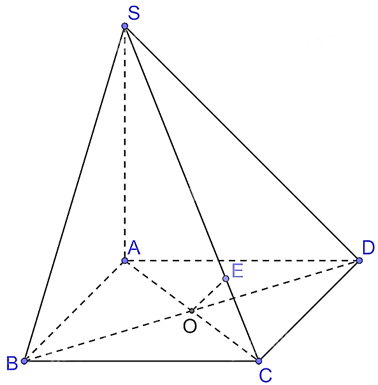
Bài 32 trang 109 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA $⊥$ (ABCD) và SA = a $\sqrt{2}$ . Mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng SC, cắt các cạnh SC, SB, SD lần lượt tại M, E, F.

a) Chứng minh AE $⊥$ (SBC).

b) Tính theo a thể tích khối chóp S.ABCD và hình chóp S.AEMF.

Lời giải:

Bài 32 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Gọi O là giao điểm của AC và BD. Kẻ AM $⊥$ SC tại M, SO $\cap$ AM = I.

Do ABCD là hình vuông nên AC $⊥$ BD.

Vì SA $⊥$ (ABCD) nên SA $⊥$ BD mà AC $⊥$ BD nên BD $⊥$ (SAC), suy ra BD $⊥$ SC.

Trong mặt phẳng (SBD), qua I kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại E và F. Khi đó (P) = (AEMF).

Do ABCD là hình vuông nên BC $⊥$ AB, SA $⊥$ BC (do SA $⊥$ (ABCD)) nên BC $⊥$ (SAB), suy ra BC $⊥$ AE.

Mặt khác SC $⊥$ (P) nên SC $⊥$ AE mà BC $⊥$ AE nên AE $⊥$ (SBC).

b) Ta có $V_{S . A B C D} = \frac{1}{3} \cdot S_{A B C D} \cdot S A$ $= \frac{1}{3} \cdot a^{2} \cdot a \sqrt{2} = \frac{a^{3} \sqrt{2}}{3}$ .

Xét tam giác SAB vuông tại A, có $S B = \sqrt{S A^{2} + A B^{2}} = \sqrt{2 a^{2} + a^{2}} = a \sqrt{3}$ .

Xét tam giác SAD vuông tại A, có $S D = \sqrt{S A^{2} + A D^{2}} = \sqrt{2 a^{2} + a^{2}} = a \sqrt{3}$ .

Xét tam giác ABC vuông tại B, có $A C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + a^{2}} = a \sqrt{2}$ .

Vì SA $⊥$ (ABCD) nên SA $⊥$ AC hay tam giác SAC vuông tại A.

Xét tam giác SAC vuông tại A, có $S C = \sqrt{S A^{2} + A C^{2}} = \sqrt{2 a^{2} + 2 a^{2}} = 2 a$ .

Có AE $⊥$ (SBC) nên AE $⊥$ SB.

Xét tam giác SAB vuông tại A, AE là đường cao nên SA² = SE . SB.

Có $\frac{S E}{S B} = \frac{S E \cdot S B}{S B^{2}} = \frac{S A^{2}}{S B^{2}} = \frac{2 a^{2}}{3 a^{2}} = \frac{2}{3}$ .

Xét tam giác SAC vuông tại A, AM là đường cao nên SA² = SM.SC.

Có $\frac{S M}{S C} = \frac{S M \cdot S C}{S C^{2}} = \frac{S A^{2}}{S C^{2}} = \frac{2 a^{2}}{4 a^{2}} = \frac{1}{2}$ .

Do ABCD là hình vuông nên DC $⊥$ AD mà SA $⊥$ DC (do SA $⊥$ (ABCD)) nên DC $⊥$ (SAD), suy ra DC $⊥$ AF.

Mặt khác SC $⊥$ (P) nên SC $⊥$ AF mà DC $⊥$ AF nên AF $⊥$ (SCD), suy ra AF $⊥$ SD.

Xét tam giác SAD vuông tại A, AF là đường cao nên SA² = SF . SD.

Có $\frac{S F}{S D} = \frac{S F \cdot S D}{S D^{2}} = \frac{S A^{2}}{S D^{2}} = \frac{2 a^{2}}{3 a^{2}} = \frac{2}{3}$ .

Ta có $\frac{V_{S.AMF}}{V_{S . A C D}} = \frac{S A}{S A} \cdot \frac{S M}{S C} \cdot \frac{S F}{S D}$ $= 1 \cdot \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3}$ $\Rightarrow V_{S.AMF} = \frac{1}{3} V_{S . A C D}$ .

$\frac{V_{S.AME}}{V_{S . A C B}} = \frac{S A}{S A} \cdot \frac{S M}{S C} \cdot \frac{S E}{S B}$ $= 1 \cdot \frac{1}{2} \cdot \frac{2}{3} = \frac{1}{3}$ $\Rightarrow V_{S.AME} = \frac{1}{3} V_{S . A C B}$ .

Suy ra $V_{S.AMF} + V_{S.AME} = \frac{1}{3} V_{S . A C D} + \frac{1}{3} V_{S . A C B}$ $\Rightarrow V_{S.AEMF} = \frac{1}{3} (V_{S . A C D} + V_{S . A C B})$

$\Rightarrow V_{S.AEMF} = \frac{1}{3} V_{S . A B C D}$ $\Rightarrow V_{S.AEMF} = \frac{1}{3} \cdot \frac{a^{3} \sqrt{2}}{3} = \frac{a^{3} \sqrt{2}}{9}$

Vậy $V_{S . A B C D} = \frac{a^{3} \sqrt{2}}{3}$ ; $V_{S.AEMF} = \frac{a^{3} \sqrt{2}}{9}$ .

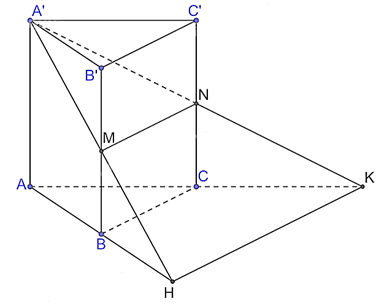
Bài 33 trang 109 Toán 11 Tập 2: Cho hình lăng trụ tam giác đều ABC.A'B'C' có AB = a, AA' = a $\sqrt{2}$ . Gọi M, N lần lượt là trung điểm của cạnh BB' và CC'. Mặt phẳng (A'MN) cắt đường thẳng AB, AC tương ứng tại H và K.

a) Chứng minh rằng MN // HK.

b) Tính theo a thể tích khối chóp A'.AHK.

Lời giải:

Bài 33 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Vì M, N lần lượt là trung điểm của cạnh BB' và CC' nên MN // BC, suy ra MN // (ABC).

Mà (ABC) $\cap$ (A'MN) = HK, suy ra MN // HK.

b) Xét $∆$ A'B'M và $∆$ HBM có

B'M = BM (do M là trung điểm của BB'),

$\hat{A^{'} B^{'} M} = \hat{H B M} = 90 °$ ,

$\hat{A^{'} M B^{'}} = \hat{H M B}$ (đối đỉnh)

Do đó, $∆$ A'B'M = $∆$ HBM.

Suy ra BH = A'B' mà AB = A'B' (do ABB'A' là hình chữ nhật) nên BH = AB = a.

Suy ra AH = 2a.

Xét $∆$ A'C'N và $∆$ KCN có

C'N = CN (do N là trung điểm của CC'),

$\hat{A^{'} C^{'} N} = \hat{K C N} = 90 °$ , $\hat{A^{'} N C^{'}} = \hat{K N C}$ (đối đỉnh)

Do đó, $∆$ A'C'N = $∆$ KCN, suy ra CK = A'C' mà A'C' = AC (do ACC'A' là hình chữ nhật) nên CK = AC = a, suy ra AK = 2a.

Xét tam giác AHK có B là trung điểm AH, C là trung điểm AK nên BC là đường trung bình của tam giác AHK, suy ra HK = 2BC = 2a.

Xét tam giác AHK có AH = AK = HK = 2a nên tam giác AHK đều, suy ra $S_{A H K} = \frac{{(2 a)}^{2} \cdot \sqrt{3}}{4} = a^{2} \sqrt{3}$ .

Khi đó $V_{A^{'} . A H K} = \frac{1}{3} \cdot \cdot S_{A H K} = \frac{1}{3} \cdot a \sqrt{2} \cdot a^{2} \sqrt{3} = \frac{a^{3} \sqrt{6}}{3}$ .

Vậy $V_{A^{'} . A H K} = \frac{a^{3} \sqrt{6}}{3}$ .

Bài 34 trang 109 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và $\hat{B A D} = 60 °$ . Biết SA $⊥$ (ABCD) và SA = a.

a) Chứng minh rằng BD $⊥$ SC.

b) Tính theo a khoảng cách giữa hai đường thẳng BD và SC.

Lời giải:

Bài 34 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Vì ABCD là hình thoi nên AC $⊥$ BD.

Vì SA $⊥$ (ABCD) nên SA $⊥$ BD mà AC $⊥$ BD nên BD $⊥$ (SAC), suy ra BD $⊥$ SC.

b) Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC, BD.

Kẻ OE $⊥$ SC tại E.

Vì BD $⊥$ (SAC) nên BD $⊥$ OE mà OE $⊥$ SC nên d(BD, SC) = OE.

Xét tam giác ABD có AB = AD = a nên tam giác ABD cân tại A mà $\hat{B A D} = 60 °$ nên tam giác ABD đều.

Xét tam giác đều ABD cạnh a có AO là đường cao nên AO = $\frac{a \sqrt{3}}{2} \Rightarrow$ AC = 2AO = a $\sqrt{3}$ .

Vì SA $⊥$ (ABCD) nên SA $⊥$ AC hay tam giác SAC vuông tại A.

Xét tam giác SAC vuông tại A, có $S C = \sqrt{S A^{2} + A C^{2}} = \sqrt{a^{2} + 3 a^{2}} = 2 a$ .

Vì O là trung điểm của AC nên CO = AO = $\frac{a \sqrt{3}}{2}$ .

Xét $∆$ CEO và $∆$ CAS có: $\hat{C}$ chung và $\hat{C E O} = \hat{CAS} = 90 °$ nên $∆$ CEO đồng dạng với $∆$ CAS, suy ra $\frac{C O}{C S} = \frac{E O}{S A}$ $\Rightarrow E O = \frac{C O \cdot S A}{C S}$ $= \frac{\frac{a \sqrt{3}}{2} \cdot a}{2 a} = \frac{a \sqrt{3}}{4}$ .

Vậy d(BD, SC) = $\frac{a \sqrt{3}}{4}$ .

Bài 35 trang 109 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AD = a, AB = a $\sqrt{2}$ . Biết SA $⊥$ (ABCD) và SA = a $\sqrt{3}$ . Gọi M là trung điểm của cạnh CD.

a) Chứng minh rằng BD $⊥$ (SAM).

b) Tính theo a thể tích khối chóp S.ABMD.

Lời giải:

Bài 35 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Do ABCD là hình chữ nhật nên AB = DC = a $\sqrt{2}$ ; AD = BC = a.

Gọi E là giao điểm của AM và BD.

Vì M là trung điểm của CD nên DM = MC = $\frac{C D}{2} = \frac{a \sqrt{2}}{2}$ .

Xét tam giác ADM vuông tại D có: $\tan \hat{A M D} = \frac{A D}{D M} = \frac{a}{\frac{a \sqrt{2}}{2}} = \sqrt{2}$ .

Xét tam giác ADB vuông tại A có: $\tan \hat{A D B} = \frac{A B}{A D} = \frac{a \sqrt{2}}{a} = \sqrt{2}$ .

Vì $\tan \hat{A M D} = \tan \hat{A D B} = \sqrt{2}$ , suy ra $\hat{A M D} = \hat{A D B}$ .

Có $\hat{A M D} + \hat{B D M} = \hat{A D B} + \hat{B D M} = \hat{A D C} = 90 °$ , suy ra $\hat{D E M} = 90 °$ hay AM $⊥$ BD.

Vì SA $⊥$ (ABCD) nên SA $⊥$ BD mà AM $⊥$ BD nên BD $⊥$ (SAM).

b) Có S_ABMD = S_ABCD – S_BCM = AB.AD - $\frac{1}{2}$ .BC.CM

= $= a \sqrt{2} \cdot a - \frac{1}{2} \cdot a \cdot \frac{a \sqrt{2}}{2} = \frac{3 a^{2} \sqrt{2}}{4}$ .

Khi đó $V_{S . A B M D} = \frac{1}{3} \cdot S_{A B M D} \cdot S A$ $= \frac{1}{3} \cdot \frac{3 a^{2} \sqrt{2}}{4} \cdot a \sqrt{3} = \frac{a^{3} \sqrt{6}}{4}$ .

Vậy $V_{S . A B M D} = \frac{a^{3} \sqrt{6}}{4} .$

Bài 36 trang 109 Toán 11 Tập 2: Trong đại dịch Covid-19, một doanh nghiệp muốn hỗ trợ các gia đình thuộc nhóm 25% hộ gia đình có thu nhập thấp nhất ở một địa phương. Một mẫu số liệu ghép nhóm về thu nhập của các hộ gia đình ở địa phương này được cho trong bảng sau:

Bài 36 trang 109 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

Dựa trên mẫu số liệu trên, hãy xác định hộ gia đình có thu nhập dưới bao nhiêu sẽ nhận được hỗ trợ của doanh nghiệp đó?

Lời giải:

Dựa vào bảng số liệu, ta tính được n = 8 + 17 + 35 + 56 + 27 + 15 = 158.

Giả sử x₁; x₂; …; x₁₅₈ là mẫu số liệu đã được sắp xếp theo thứ tự không giảm. Khi đó trung vị là $\frac{x_{79} + x_{80}}{2}$ và tứ phân vị thứ nhất là x₄₀.

Do đó, nhóm chứa tứ phân vị thứ nhất Q₁ là nhóm thứ 3: [8; 11).

Có a₃ = 8; m₃ = 35; m₁ = 8; m₂ = 17; a₄ = 11.

Áp dụng công thức tính tứ phân vị thứ nhất Q₁, ta có

$Q_{1} = a_{3} + \frac{\frac{n}{4} - (m_{1} + m_{2})}{m_{3}} \cdot (a_{4} - a_{3})$ $= 8 + \frac{\frac{158}{4} - (8 + 17)}{35} \cdot (11 - 8)$ $\approx$ 9,24.

Vậy doanh nghiệp sẽ hỗ trợ hộ gia đình có thu nhập dưới 9,24 triệu đồng.

Bài 37 trang 109 Toán 11 Tập 2: Hai bạn Dũng và Cường tham gia một kì thi học sinh giỏi môn Toán. Xác suất để Dũng và Cường đạt giải tương ứng là 0,85 và 0,9. Tính xác suất để:

a) Có ít nhất một trong hai bạn đạt giải;

b) Có đúng một bạn đạt giải.

Lời giải:

Gọi biến cố A: “Dũng đạt giải”;

Biến cố B: “Cường đạt giải”;

A $\cup$ B: “Có ít nhất một bạn được giải”.

$\bar{A B}$ : “Không có bạn nào đạt giải”;

Theo đề, có P(A) = 0,85; P(B) = 0,9.

Vì A, B độc lập nên P(AB) = P(A) . P(B) = 0,85 . 0,9 = 0,765.

P( $\bar{A B}$ ) = P( $\bar{A}$ ).P( $\bar{B}$ ) = (1-P(A)).(1-P(B)) = (1 – 0,85).(1 – 0,9) = 0,015.

a) Ta cần tính P(A $\cup$ B). Biến cố đối của biến cố “Có ít nhất một bạn được giải” là biến cố “Không có bạn nào đạt giải” nên ta có

$P (A \cup B) = 1 - P (\bar{A B}) =$ 1 - 0,015 = 0,985.

Vậy xác suất để có ít nhất một trong hai bạn đạt giải là 0,985.

b) Gọi biến cố E: “Có đúng một bạn đạt giải”.

Ta có E = A $\bar{B}$ $\cup$ $\bar{A}$ B. Do A và B độc lập nên A và $\bar{B}$ ; $\bar{A}$ và B cũng độc lập.

Do đó

P(E) = P(A $\bar{B}$ $\cup$ $\bar{A}$ B) = P(A $\bar{B}$ )+P( $\bar{A}$ B)

= P(A).P( $\bar{B}$ ) + P( $\bar{A}$ ).P(B)

= 0,85 . (1 – 0,9) + (1 – 0,85) . 0,9 = 0,22.

Vậy xác suất để có đúng một bạn đạt giải là 0,22.

Bài 38 trang 109 Toán 11 Tập 2: Một máy bay có 4 động cơ trong đó 2 động cơ ở cánh phải và 2 động cơ ở cánh trái. Chuyến bay hạ cánh an toàn khi trên mỗi cánh của nó có ít nhất một động cơ không bị lỗi. Giả sử mỗi động cơ ở cánh phải có xác suất bị lỗi là 0,01 và mỗi động cơ ở cánh trái có xác suất bị lỗi là 0,015. Các động cơ hoạt động độc lập với nhau. Tính xác suất để chuyến bay hạ cánh an toàn.

Lời giải:

Gọi biến cố E: “Cánh phải có ít nhất một động cơ không bị lỗi”;

Biến cố F: “Cánh trái có ít nhất một động cơ không bị lỗi”;

Biến cố $\bar{E}$ : “Cả hai động cơ ở cánh phải đều bị lỗi”;

Biến cố $\bar{F}$ : “Cả hai động cơ ở cánh trái đều bị lỗi”.

Biến cố M: “Chuyến bay hạ cánh an toàn”.

Vì các động cơ hoạt động độc lập với nhau nên ta có:

P( $\bar{E}$ ) = 0,01.0,01 = 10^-4; P( $\bar{F}$ ) = 0,015.0,015 = 2,25.10^-4.

Suy ra P(E) = 1-P( $\bar{E}$ ) = 0,9999; P(F) = 1 - P( $\bar{F}$ ) = 0,999775.

Vì E, F là các biến cố độc lập nên P(M) = P(EF) = P(E) . P(F) = 0,9999 . 0,999775 $\approx$ 0,9997.

Vậy xác suất để chuyến bay đó hạ cánh an toàn khoảng 0,9997.

Lời giải bài tập Toán 11 Bài tập ôn tập cuối năm Kết nối tri thức hay khác:

Xem thêm lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán 11 Kết nối tri thức

Giải Toán 11 trang 109 Tập 2 Kết nối tri thức

Giải Toán 11 trang 109 Tập 2 Kết nối tri thức

Xem thêm lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác: