Giải Toán 11 trang 25 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 25 Tập 2 trong Bài tập cuối chương 6 Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 25.

Giải Toán 11 trang 25 Tập 2 Kết nối tri thức

Bài 6.27 trang 25 Toán 11 Tập 2: Cho hai số thực dương x, y và hai số thực α, β tùy ý. Khẳng định nào sau đây là sai?

A. x^α ∙ x^β = x^{α + β}.

B. x^α ∙ y^β = (xy)^{α + β}.

C. (x^α)^β = x^{α ∙ β}.

D. (xy)^α = x^α ∙ y^α.

Lời giải:

Đáp án đúng là: B

Không có công thức lũy thừa cho hai lũy thừa không cùng số mũ và không cùng cơ số, do đó đáp án B sai.

Bài 6.28 trang 25 Toán 11 Tập 2: Rút gọn biểu thức $\sqrt{x\sqrt{x\sqrt{x}}}:x^{\frac{5}{8}}\left(x>0\right)$ ta được

A. $\sqrt[4]{x}$.

B. $\sqrt{x}$.

C. $\sqrt[3]{x}$.

D. $\sqrt[5]{x}$.

Lời giải:

Đáp án đúng là: A

Với x > 0, ta có:

$\sqrt{x\sqrt{x\sqrt{x}}}:x^{\frac{5}{8}}=\sqrt{x\sqrt{x\cdot x^{\frac{1}{2}}}}:x^{\frac{5}{8}}=\sqrt{x\sqrt{x^{\frac{3}{2}}}}:x^{\frac{5}{8}}$

$=\sqrt{x\cdot {\left(x^{\frac{3}{2}}\right)}^{\frac{1}{2}}}:x^{\frac{5}{8}}=\sqrt{x\cdot x^{\frac{3}{4}}}:x^{\frac{5}{8}}=\sqrt{x^{\frac{7}{4}}}:x^{\frac{5}{8}}$

$={\left(x^{\frac{7}{4}}\right)}^{\frac{1}{2}}:x^{\frac{5}{8}}=x^{\frac{7}{8}}:x^{\frac{5}{8}}=x^{\frac{1}{4}}=\sqrt[4]{x}$.

Bài 6.29 trang 25 Toán 11 Tập 2: Cho hai số thực dương a, b với a ≠ 1. Khẳng định nào sau đây là đúng?

A. log_a(a³b²) = 3 + log_ab.

B. log_a(a³b²) = 3 + 2log_ab.

C. log_a(a³b²) = $\frac{3}{2}$ log_ab.

D. log_a(a³b²) = $\frac{1}{3}+\frac{1}{2}{\log }_{a}b$.

Lời giải:

Đáp án đúng là: B

Ta có log_a(a³b²) = log_aa³ + log_ab² = 3 + 2log_ab.

Bài 6.30 trang 25 Toán 11 Tập 2: Cho bốn số thực dương a, b, x, y với a, b ≠ 1. Khẳng định nào sau đây là sai?

A. log_a(xy) = log_ax + log_ay.

B. ${\log }_a\frac{x}{y}={\log }_{a}x-{\log }_{a}y$.

C. ${\log }_a\frac{1}{x}=\frac{1}{{\log }_{a}x}$.

D. log_ab ∙ log_bx = log_ax.

Lời giải:

Đáp án đúng là: C

Theo tính chất của lôgarit, ta thấy các công thức ở các đáp án A, B, D đúng.

Với đáp án C, ta có ${\log }_a\frac{1}{x}={\log }_a{x}^{-1}=-{\log }_{a}x$.

Bài 6.31 trang 25 Toán 11 Tập 2: Đặt log₂5 = a, log₃5 = b. Khi đó, log₆5 tính theo a và b bằng

A. $\frac{ab}{a+b}$.

B. $\frac{1}{a+b}$.

C. a² + b².

D. a + b.

Lời giải:

Đáp án đúng là: A

Ta có log₆5 = $\frac{1}{{\log }_{5}6}=\frac{1}{{\log }_5\left(2\cdot 3\right)}=\frac{1}{{\log }_{5}2+{\log }_{5}3}$

$=\frac{1}{\frac{1}{{\log }_{2}5}+\frac{1}{{\log }_{3}5}}=\frac{1}{\frac{1}{a}+\frac{1}{b}}=\frac{1}{\frac{b+a}{ab}}=\frac{ab}{a+b}$.

Bài 6.32 trang 25 Toán 11 Tập 2: Cho hàm số y = 2^x. Khẳng định nào sau đây là sai?

A. Tập xác định của hàm số là ℝ.

B. Tập giá trị của hàm số là (0; + ∞).

C. Đồ thị của hàm số cắt trục Ox tại đúng một điểm.

D. Hàm số đồng biến trên tập xác định của nó.

Lời giải:

Đáp án đúng là: C

Ta có hàm số y = 2^x_­:

+ Có tập xác định là ℝ.

+ Có tập giá trị của hàm số là (0; + ∞).

+ Đồng biến trên ℝ (do 2 > 1).

+ Đồ thị của hàm số luôn nằm phía trên trục Ox.

Do vậy đáp án C sai.

Bài 6.33 trang 25 Toán 11 Tập 2: Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. y = log_0,5­x.

B. y = e^{– x}.

C. $y={\left(\frac{1}{3}\right)}^x$.

D. y = ln x.

Lời giải:

Đáp án đúng là: D

Xét từng đáp án:

+ Hàm số y = log_0,5­x có tập xác định là (0; + ∞) và nghịch biến trên (0; + ∞) (do 0 < 0,5 < 1).

+ Hàm số y = e^{– x} = ${\left(\frac{1}{e}\right)}^x$ có tập xác định là ℝ và nghịch biến trên ℝ do $0<\frac{1}{e}<1$.

+ Hàm số $y={\left(\frac{1}{3}\right)}^x$ có tập xác định là ℝ và nghịch biến trên ℝ do $0<\frac{1}{3}<1$.

+ Hàm số y = ln x có tập xác định là (0; + ∞) và đồng biến trên (0; + ∞) do e > 1.

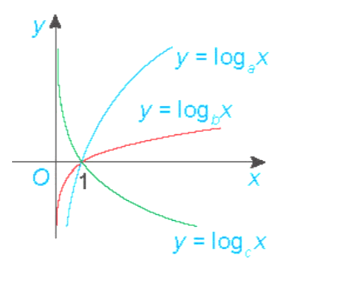
Bài 6.34 trang 25 Toán 11 Tập 2: Cho đồ thị ba hàm số y = log_ax, y = log_bx và y = log_cx như hình bên. Mệnh đề nào sau đây là đúng?

A. a > b > c.

B. b > a > c.

C. a > c > b.

D. b > c > a.

Lời giải:

Quan sát đồ thị ta thấy:

+ Hàm số y = log_ax và y = log_bx đồng biến trên (0; + ∞) nên a, b > 1.

+ Hàm số y = log_cx nghịch biến trên (0; + ∞) nên c < 1.

+ Với x > 1, ta có log_ax > log_bx $\iff \frac{1}{{\log }_{a}x}<\frac{1}{{\log }_{b}x}$⇔ log_xa < log_xb ⇔ a < b.

Vậy c < a < b hay b > a > c.

Lời giải bài tập Toán 11 Bài tập cuối chương 6 Kết nối tri thức hay khác:

• Giải Toán 11 trang 26