Giải Toán 11 trang 40 Tập 2 Kết nối tri thức
Với Giải Toán 11 trang 40 Tập 2 trong Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 40.
Giải Toán 11 trang 40 Tập 2 Kết nối tri thức
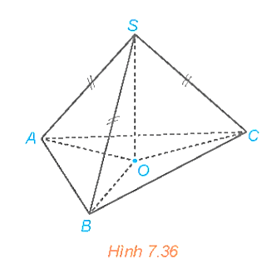
Luyện tập 1 trang 40 Toán 11 Tập 2: Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).
a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.
b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC).
c) Chứng minh rằng nếu thì .
d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC).
Lời giải:
a) Vì O là hình chiếu của S trên mặt phẳng (ABC) nên SO ⊥ (ABC), suy ra SO ⊥ OA, SO ⊥ OB, SO ⊥ OC.
Xét tam giác SOA vuông tại O, có SO2 + OA2 = SA2.
Xét tam giác SOB vuông tại O, có SO2 + OB2 = SB2.
Xét tam giác SOC vuông tại O, có SO2 + OC2 = SC2.
Mà SA = SB = SC nên OA = OB = OC hay O là tâm đường tròn ngoại tiếp tam giác ABC.
b) O là hình chiếu của S trên mặt phẳng (ABC), A là hình chiếu của A trên mặt phẳng (ABC). Do đó OA là hình chiếu của SA trên mặt phẳng (ABC).
c) Vì SO ⊥ (ABC) nên SO ⊥ BC mà AO ⊥ BC nên BC ⊥ (SAO), suy ra BC ⊥ SA.
d) O là hình chiếu của S trên mặt phẳng (ABC).
A là hình chiếu của A trên mặt phẳng (ABC).
B là hình chiếu của B trên mặt phẳng (ABC).
C là hình chiếu của C trên mặt phẳng (ABC).
Do đó hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC) lần lượt là: OBC, OCA, OAB.
HĐ3 trang 40 Toán 11 Tập 2: Một máy bay giữ vận tốc không đổi, với độ lớn 240 km/h trong suốt 2 phút đầu kể từ khi cất cánh. Hỏi thông tin trên có đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh không?
Lời giải:
Thông tin trên chưa đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh.
Lời giải bài tập Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng Kết nối tri thức hay khác: