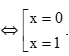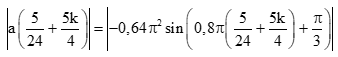Giải Toán 11 trang 97 Tập 2 Kết nối tri thức

---

Với Giải Toán 11 trang 97 Tập 2 trong Bài tập cuối chương 9 Toán lớp 11 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 97.

Giải Toán 11 trang 97 Tập 2 Kết nối tri thức

Bài 9.18 trang 97 Toán 11 Tập 2: Với u, v là các hàm số hợp theo biến x, quy tắc tính đạo hàm nào sau đây là đúng?

A. (u + v)' = u' – v'.

B. (uv)' = u'v + uv'.

C. ${\left(\frac{1}{v}\right)}^{\text{'}}=-\frac{1}{v^2}$ .

D. ${\left(\frac{u}{v}\right)}^{\text{'}}=\frac{u^{\text{'}}v+v^{\text{'}}u}{v^2}$ .

Lời giải:

Đáp án đúng là: B

Ta có quy tắc đạo hàm:

(u + v)' = u' + v'

(uv)' = u'v + uv'

${\left(\frac{1}{v}\right)}^{\text{'}}=-\frac{v^{\text{'}}}{v^2}$

${\left(\frac{u}{v}\right)}^{\text{'}}=\frac{u^{\text{'}}v-v^{\text{'}}u}{v^2}$

Vậy đáp án B đúng.

Bài 9.19 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = x² + sin³x. Khi đó $f^{\text{'}}\left(\frac{\pi }{2}\right)$ bằng

A. π.

B. 2π.

C. π + 3.

D. π – 3.

Lời giải:

Đáp án đúng là: A

Ta có: f'(x) = 2x + 3sin²xcosx

$\Rightarrow f^{\text{'}}\left(\frac{\pi }{2}\right)=2.\frac{\pi }{2}+2.{\sin }^2\frac{\pi }{2}.\cos \frac{\pi }{2}=\pi$.

Bài 9.20 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = $\frac{1}{3}{x}^3-x^2-3x+1$ . Tập nghiệm của bất phương trình f'(x) ≤ 0 là

A. [1; 3].

B. [–1; 3].

C. [–3; 1].

D. [–3; –1].

Lời giải:

Đáp án đúng là: B

Ta có f'(x) = x² – 2x – 3.

Khi đó f'(x) ≤ 0 ⇔ x² – 2x – 3 ≤ 0 ⇔ –1 ≤ x ≤ 3.

Bài 9.21 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = $\sqrt{4+3u\left(x\right)}$ với u(1) = 7, u'(1) = 10. Khi đó f'(1) bằng

A. 1.

B. 6.

C. 3.

D. –3.

Lời giải:

Đáp án đúng là: C

Ta có f'(x) = $\frac{3u^{\text{'}}\left(x\right)}{2\sqrt{4+3u\left(x\right)}}$.

Nên f'(1) = $\frac{3u^{\text{'}}\left(1\right)}{2\sqrt{4+3u\left(1\right)}}=\frac{3.10}{2\sqrt{4+3.7}}=3$ .

Bài 9.22 trang 97 Toán 11 Tập 2: Cho hàm số f(x) = x²e^–2x. Tập nghiệm của phương trình f'(x) = 0 là

A. {0; 1}.

B. {–1; 0}.

C. {0}.

D. {1}.

Lời giải:

Đáp án đúng là: A

Ta có f'(x) = (x²)' . e^{– 2x} + x² . (e^{– 2x})' = 2xe^–2x – 2x²e^–2x.

Để f'(x) = 0 ⇔ 2xe^–2x – 2x²e^–2x = 0

⇔ 2xe^–2x(1 – x) = 0

Bài 9.23 trang 97 Toán 11 Tập 2: Chuyển động của một vật có phương trình s(t) = sin$\left(0,8\pi t+\frac{\pi }{3}\right)$, ở đó s tính bằng centimét và thời gian t tính bằng giây. Tại các thời điểm vận tốc bằng 0, giá trị tuyệt đối của gia tốc của vật gần với giá trị nào sau đây nhất?

A. 4,5 cm/s².

B. 5,5 cm/s².

C. 6,3 cm/s².

D. 7,1 cm/s².

Lời giải:

Đáp án đúng là: C

Ta có: v(t) = s'(t) = 0,8πcos$\left(0,8\pi t+\frac{\pi }{3}\right)$;

a(t) = s''(t) = –0,8π.0,8πsin$\left(0,8\pi t+\frac{\pi }{3}\right)$ = –0,64π²sin$\left(0,8\pi t+\frac{\pi }{3}\right)$ .

Ta có v(t) = 0

$\iff 0,8\pi \cos \left(0,8\pi t+\frac{\pi }{3}\right)=0$

$\iff 0,8\pi t+\frac{\pi }{3}=\frac{\pi }{2}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff 0,8\pi t=\frac{\pi }{2}-\frac{\pi }{3}+k\pi \left(k\in \mathbb{Z}\right)$

$\iff t=\frac{5}{24}+\frac{5k}{4}\left(k\in \mathbb{Z}\right)$

Thời điểm vận tốc bằng 0 giá trị tuyệt đối của gia tốc của vật là:

$=0,64{\pi }^2$$=0,64{\pi }^2\approx 6,32$.

Bài 9.24 trang 97 Toán 11 Tập 2: Cho hàm số y = x³ – 3x² + 4x – 1 có đồ thị là (C). Hệ số góc nhỏ nhất của tiếp tuyến tại một điểm M trên đồ thị (C) là

A. 1.

B. 2.

C. –1.

D. 3.

Lời giải:

Đáp án đúng là: A

Hệ số góc của tiếp tuyến tại một điểm M trên đồ thị (C) là

k = y' = 3x² – 6x + 4 = 3(x² – 2x + 1) + 1 = 3(x – 1)² + 1 ≥ 1 với mọi x.

Vậy hệ số góc nhỏ nhất của tiếp tuyến tại một điểm M trên đồ thị (C) là 1.

Bài 9.25 trang 97 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau:

a) $y={\left(\frac{2x-1}{x+2}\right)}^5$ ;

b) $y=\frac{2x}{x^2+1}$ ;

c) y = e^xsin²x;

d) y = log(x+$\sqrt{x}$).

Lời giải:

a) Với x ≠ – 2, ta có

$y^{\text{'}}=5{\left(\frac{2x-1}{x+2}\right)}^4.{\left(\frac{2x-1}{x+2}\right)}^{\text{'}}=5{\left(\frac{2x-1}{x+2}\right)}^4.\frac{2\left(x+2\right)-\left(2x-1\right)}{{\left(x+2\right)}^2}$

$=5{\left(\frac{2x-1}{x+2}\right)}^4.\frac{5}{{\left(x+2\right)}^2}=\frac{25{\left(2x-1\right)}^4}{{\left(x+2\right)}^6}$.

b) Ta có

$y^{\text{'}}=\frac{{\left(2x\right)}^{\text{'}}.\left(x^2+1\right)-2x{\left(x^2+1\right)}^{\text{'}}}{{\left(x^2+1\right)}^2}=\frac{2x^2+2-4x^2}{{\left(x^2+1\right)}^2}=\frac{-2x^2+2}{{\left(x^2+1\right)}^2}$.

c) Ta có

y' = (e^x)' . sin²x + e^x(sin²x)' = e^xsin²x + e^x.2sinx.cosx = e^xsin²x + e^xsin2x.

d) Với x > 0, ta có:

$y^{\text{'}}=\frac{{\left(x+\sqrt{x}\right)}^{\text{'}}}{\left(x+\sqrt{x}\right)\ln 10}=\frac{1+\frac{1}{2\sqrt{x}}}{\left(x+\sqrt{x}\right)\ln 10}=\frac{2\sqrt{x}+1}{2\sqrt{x}\left(x+\sqrt{x}\right)\ln 10}$.

Lời giải bài tập Toán 11 Bài tập cuối chương 9 Kết nối tri thức hay khác:

• Giải Toán 11 trang 98