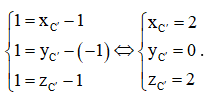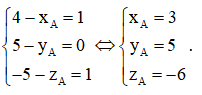Giải Toán 12 trang 71 Tập 1 Cánh diều

---

Với Giải Toán 12 trang 71 Tập 1 trong Bài 2: Toạ độ của vectơ Toán 12 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 71.

Giải Toán 12 trang 71 Tập 1 Cánh diều

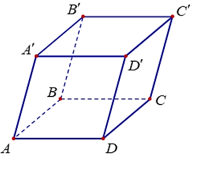
Hoạt động 6 trang 71 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(x_A; y_A; z_A), B(x_B; y_B; z_B­) (Hình 32).

a) Biểu diễn mỗi vectơ $\overrightarrow{OA},\overrightarrow{OB}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j}$ và $\overrightarrow{k}$.

b) Tìm liên hệ giữa $\overrightarrow{AB}$ và (x_B – x_A)$\overrightarrow{i}$ + (y_B – y_A)$\overrightarrow{j}$+ (z_B – z_A)$\overrightarrow{k}$.

c) Từ đó, tìm tọa độ của vectơ $\overrightarrow{AB}$ .

Lời giải:

a) Vì điểm A có tọa độ là (x_A; y_A; z_A) nên $\overrightarrow{OA}=\left(x_A;y_A;z_A\right)$ .

Do đó, $\overrightarrow{OA}=x_A\overrightarrow{i}+y_A\overrightarrow{j}+z_A\overrightarrow{k}$ .

Vì điểm B có tọa độ là (x_B; y_B; z_B­) nên $\overrightarrow{OB}=\left(x_B;y_B;z_B\right)$ .

Do đó, $\overrightarrow{OB}=x_B\overrightarrow{i}+y_B\overrightarrow{j}+z_B\overrightarrow{k}$ .

b) Theo quy tắc hiệu ta có

c) Ta có $\overrightarrow{AB}$ = (x_B – x_A)$\overrightarrow{i}$ + (y_B – y_A)$\overrightarrow{j}$+ (z_B – z_A)$\overrightarrow{k}$.

Do đó, $\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A;z_B-z_A\right)$ .

Luyện tập 6 trang 71 Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A'(1; 0; 1), B'(2; 1; 2), D'(1; – 1; 1), C(4; 5; – 5). Tìm tọa độ đỉnh A của hình hộp ABCD.A'B'C'D'.

Lời giải:

Ta có $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$ = (2 – 1; 1 – 0; 2 – 1) = (1; 1; 1).

Gọi tọa độ của điểm C' là (x_C'; y_C'; z_C'), ta có $\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$ = (x_C' – 1; y_C' – (– 1); z_C' – 1).

Vì ABCD.A'B'C'D' là hình hộp nên A'B'C'D' là hình bình hành.

Do đó, $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}=\overrightarrow{D^{\text{'}}{C}^{\text{'}}}$ . Suy ra

Khi đó, C'(2; 0; 2).

Ta có $\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ = (2 – 1; 0 – 0; 2 – 1) = (1; 0; 1).

Gọi tọa độ của điểm A là (x_A; y_A; z_A), ta có $\overrightarrow{AC}=\left(4-x_A;5-y_A;-5-z_A\right)$ .

Vì ABCD.A'B'C'D' là hình hộp nên $\overrightarrow{AC}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ .

Do đó,

Vậy A(3; 5; – 6).

Lời giải bài tập Toán 12 Bài 2: Toạ độ của vectơ hay khác:

• Giải Toán 12 trang 65

• Giải Toán 12 trang 66

• Giải Toán 12 trang 68

• Giải Toán 12 trang 69

• Giải Toán 12 trang 70

• Giải Toán 12 trang 72

• Giải Toán 12 trang 73