Bài 1.13 trang 19 Toán 12 Tập 1 - Kết nối tri thức

Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất?

Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

Bài 1.13 trang 19 Toán 12 Tập 1: Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất?

Lời giải:

Nửa chu vi hình chữ nhật là: 24 : 2 = 12 (cm)

Gọi chiều dài hình chữ nhật là x (cm) (0 < x < 12).

Khi đó chiều rộng hình chữ nhật là 12 – x (cm).

Diện tích hình chữ nhật là x(12 – x) = 12x – x² (cm²).

Bài toán trở thành tìm giá trị lớn nhất của hàm số y = 12x – x² (0 < x < 12).

Có y' = 12 – 2x; y' = 0 ⇔ x = 6.

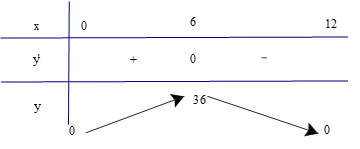
Lập bảng biến thiên của hàm số

Bài 1.13 trang 19 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Dựa vào bảng biến thiên, ta có diện tích lớn nhất hình chữ nhật là 36 cm² khi nó là hình vuông có cạnh bằng 6 cm.

Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết khác: