Vận dụng trang 18 Toán 12 Tập 1 - Kết nối tri thức
Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số N(t) = −t + 12t, 0 £ t £ 12, trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).
Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức
Vận dụng trang 18 Toán 12 Tập 1: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số N(t) = −t3 + 12t2, 0 £ t £ 12, trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).
Lời giải:
a) Có N'(t) = −3t2 + 24t; N'(t) = 0 ⇔ t = 0 hoặc t = 8.
Có N(0) = 0; N(8) = 256; N(12) = 0.
Vậy giá trị lớn nhất của hàm số là N(8) = 256.
Vậy số người tối đa bị nhiễm ở địa phương đó là 256 người.
b) Có N'(t) = −3t2 + 24t.
Để xác định thời điểm virus lây nhanh nhất, ta sẽ đi tìm điểm cực đại của N'(t).
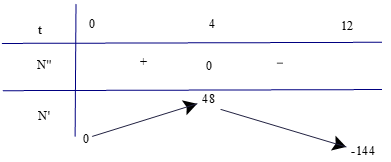
Có N"(t) = −6t + 24; N"(t) = 0 ⇔ t = 4.
Lập bảng biến thiên
Dựa vào bảng biến thiên, ta có virus lây lan nhanh nhất vào thời điểm t = 4 tuần.
Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết khác:
Luyện tập 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau ....