Bài 1.14 trang 19 Toán 12 Tập 1 - Kết nối tri thức

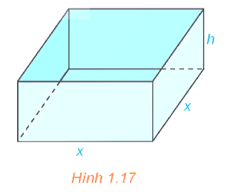
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Kết nối tri thức

Bài 1.14 trang 19 Toán 12 Tập 1: Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm² như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

Lời giải:

Thể tích của chiếc hộp là V = x².h (cm³).

Vì diện tích bề mặt bằng 108 cm² nên ta có:

x² + 4xh = 108

⇔ $h=\frac{108-x^2}{4x}$ (điều kiện $0<x<\sqrt{108}$).

Khi đó thể tích chiếc hộp là $V=\frac{x\left(108-x^2\right)}{4}=-\frac{x^3}{4}+27x$.

Bài toán trở thành tìm giá trị lớn nhất của hàm số $V=-\frac{x^3}{4}+27x\left(0<x<\sqrt{108}\right)$.

Có $V^{\text{'}}=-\frac{3}{4}{x}^2+27$; V' = 0$\iff -\frac{3}{4}{x}^2+27=0\iff x=6$(vì $0<x<\sqrt{108}$)

Lập bảng biến thiên của hàm số

Dựa vào bảng biến thiên, ta có thể tích lớn nhất của chiếc hộp là 108 cm³ khi x = 6cm và h = 3cm.

Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay, chi tiết khác:

• Mở đầu trang 15 Toán 12 Tập 1: Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông ....

• HĐ1 trang 15 Toán 12 Tập 1: Cho hàm số y = f(x) = x² – 2x với x ∈ [0; 3], có đồ thị như hình 1.15 ....

• Luyện tập 1 trang 17 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau ....

• HĐ2 trang 17 Toán 12 Tập 1: Xét hàm số y = f(x) = x³ – 2x² + 1 trên đoạn [−1; 2] với đồ thị như hình 1.16 ....

• Luyện tập 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau ....

• Vận dụng trang 18 Toán 12 Tập 1: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa ....

• Bài 1.10 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau ....

• Bài 1.11 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau ....

• Bài 1.12 trang 19 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau ....

• Bài 1.13 trang 19 Toán 12 Tập 1: Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất? ....

• Bài 1.15 trang 19 Toán 12 Tập 1: Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm³ ....