Bài 2.37 trang 74 Toán 12 Kết nối tri thức Tập 1

Cho hình hộp ABCD.A'B'C'D', gọi G là trọng tâm của tam giác BDA'.

Giải Toán 12 Bài tập cuối chương 2 - Kết nối tri thức

Bài 2.37 trang 74 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D', gọi G là trọng tâm của tam giác BDA'.

a) Biểu diễn $\vec{A G}$ theo $\vec{A B}, \vec{A D}$ và $\vec{A A^{'}}$ .

b) Từ câu a, hãy chứng tỏ ba điểm A, G và C' thẳng hàng.

Lời giải:

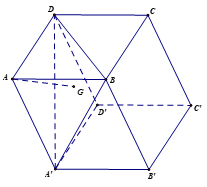
a) Vì G là trọng tâm của tam giác BDA' nên

$\vec{G B} + \vec{G D} + \vec{G A^{'}} = \vec{0}$ (1)

$\Leftrightarrow \vec{G A} + \vec{A B} + \vec{G A} + \vec{A D} + \vec{G A} + \vec{A A^{'}} = \vec{0}$

$\Leftrightarrow 3 \vec{G A} + \vec{A B} + \vec{A D} + \vec{A A^{'}} = \vec{0}$

$\Leftrightarrow \vec{A G} = \frac{1}{3} (\vec{A B} + \vec{A D} + \vec{A A^{'}})$ .

b) Vì ABCD.A'B'C'D' là hình hộp nên theo quy tắc hình hộp ta có:

$\vec{A C^{'}} = \vec{A B} + \vec{A D} + \vec{A A^{'}}$ (2).

Từ (1) và (2), ta có $\vec{A G} = \frac{1}{3} \vec{A C^{'}}$ .

Vậy ba điểm A, G và C' thẳng hàng.

Lời giải bài tập Toán 12 Bài tập cuối chương 2 hay, chi tiết khác: