Bài 4 trang 63 Toán 7 Tập 2 Chân trời sáng tạo

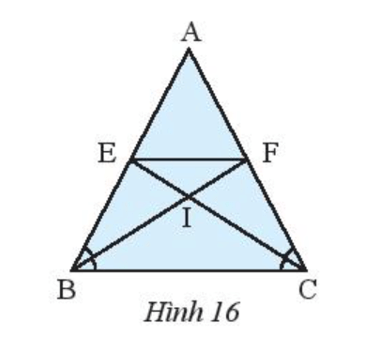
Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

Giải Toán 7 Bài 3: Tam giác cân - Chân trời sáng tạo

Bài 4 trang 63 Toán 7 Tập 2: Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

a) Chứng minh rằng $\hat{A B F} = \hat{A C E}$ .

b) Chứng minh rằng tam giác AEF cân.

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân.

Lời giải:

a) Do tam giác ABC cân tại A nên AB = AC và $\hat{A B C} = \hat{A C B}$ .

Do BF là tia phân giác của $\hat{A B C}$ nên $\hat{A B F} = \hat{F B C} = \frac{1}{2} \hat{A B C}$ .

Do CE là tia phân giác của $\hat{A C B}$ nên $\hat{A C E} = \hat{E C B} = \frac{1}{2} \hat{A C B}$ .

Do đó $\hat{A B F} = \hat{A C E}$ .

b) Xét $Δ A B F$ và $Δ A C E$ có:

$\hat{A B F} = \hat{A C E}$ (chứng minh trên).

AB = AC (chứng minh trên).

$\hat{A}$ chung.

Do đó $Δ A B F = Δ A C E$ (g.c.g).

Suy ra AF = AE (2 cạnh tương ứng).

Tam giác AEF có AF = AE nên tam giác AEF cân tại A.

c) Ta có $\hat{F B C} = \hat{E C B}$ nên $\hat{I B C} = \hat{I C B}$ .

Tam giác IBC có $\hat{I B C} = \hat{I C B}$ nên tam giác IBC cân tại I.

Do đó IB = IC.

Xét $Δ E I B$ và $Δ F I C$ có:

$\hat{E I B} = \hat{F I C}$ (đối đỉnh).

IB = IC (chứng minh trên).

$\hat{E B I} = \hat{F C I}$ (chứng minh trên).

Do đó $Δ E I B = Δ F I C$ (g.c.g).

Suy ra IE = IF (2 cạnh tương ứng).

Tam giác IEF có IE = IF nên tam giác IEF cân tại I.

Lời giải bài tập Toán 7 Bài 3: Tam giác cân hay, chi tiết khác: