Bài 7 trang 84 Toán 7 Tập 2 Chân trời sáng tạo
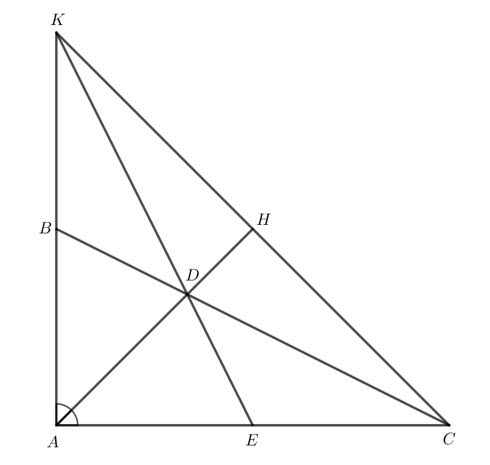
Cho tam giác ABC vuông tại A có AB = AC, AD là tia phân giác (D BC). Gọi E là trung điểm của AC.
Giải Toán 7 Bài tập cuối chương 8 - Chân trời sáng tạo
Bài 7 trang 84 Toán 7 Tập 2: Cho tam giác ABC vuông tại A có AB = AC, AD là tia phân giác (D BC). Gọi E là trung điểm của AC.
a) Chứng minh rằng DE = DB.
b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.
c) AD cắt CK tại H. Chứng minh rằng AH KC.
Lời giải:
a) Do E là trung điểm của AC nên AE = AC.
Mà AB = AC nên AE = AB.
Do AD là tia phân giác của nên .
Xét và có:
AB = AE (chứng minh trên).
(chứng minh trên).
AD chung.
Do đó (c.g.c).
Suy ra DB = DE (2 cạnh tương ứng).
b) Do (c.g.c) nên (2 góc tương ứng).
Mà (2 góc đối đỉnh) nên hay .
Xét và có:
(chứng minh trên).
AD chung.
(chứng minh trên).
Do đó (g.c.g).
Suy ra DK = DC (2 cạnh tương ứng) và AK = AC (2 cạnh tương ứng).
Tam giác DCK có DK = DC nên tam giác DCK cân tại D.
Do AK = AC, mà AC = 2AB nên AK = 2AB.
Mà A, B, K thẳng hàng nên B là trung điểm của AK.
c) Do AD là đường phân giác của nên hay (2 góc tương ứng).
Xét KAH và CAH có:
AK = AC (chứng minh trên).
(chứng minh trên).
AH chung.
Suy ra KAH = CAH (c.g.c).
Do đó (2 góc tương ứng).
Mà nên hay .
Suy ra .
Do đó AH KC.
Lời giải bài tập Toán 7 Bài tập cuối chương 8 trang 84 hay, chi tiết khác: