Bài 8 trang 84 Toán 7 Tập 2 Chân trời sáng tạo

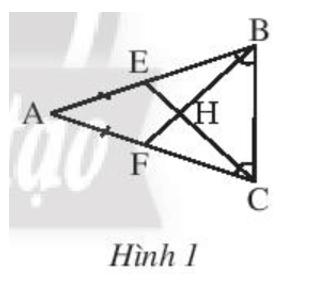
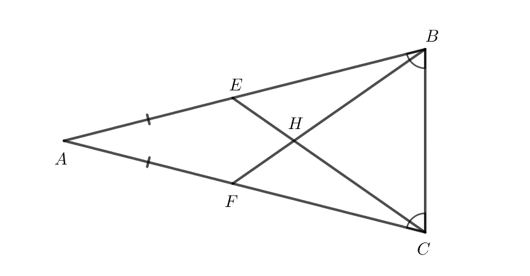
Ở Hình 1, cho biết AE = AF và . Chứng minh rằng AH là đường trung trực của BC.

Giải Toán 7 Bài tập cuối chương 8 - Chân trời sáng tạo

Bài 8 trang 84 Toán 7 Tập 2: Ở Hình 1, cho biết AE = AF và $\hat{A B C} = \hat{A C B}$ . Chứng minh rằng AH là đường trung trực của BC.

Lời giải:

Tam giác ABC có $\hat{A B C} = \hat{A C B}$ nên tam giác ABC cân tại A.

Do đó AB = AC.

Suy ra A nằm trên đường trung trực của BC (1).

Mà AE = AF nên AB - AE = AC - AF hay BE = CF.

Xét $Δ E B C$ và $Δ F C B$ có:

BE = CF (chứng minh trên).

$\hat{E B C} = \hat{F C B}$ (theo giả thiết).

BC chung.

Do đó $Δ E B C = Δ F C B$ (c.g.c).

Suy ra $\hat{E C B} = \hat{F B C}$ (2 góc tương ứng) hay $\hat{H C B} = \hat{H B C}$ .

Tam giác HBC có $\hat{H C B} = \hat{H B C}$ nên tam giác HBC cân tại H.

Do đó HB = HC.

Suy ra H nằm trên đường trung trực của BC (2).

Từ (1) và (2) suy ra AH là đường trung trực của BC.

Lời giải bài tập Toán 7 Bài tập cuối chương 8 trang 84 hay, chi tiết khác: