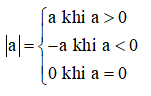Tổng hợp lý thuyết Toán 7 Chương 2 Kết nối tri thức

---

Với tổng hợp lý thuyết Toán lớp 7 Chương 2: Số thực hay nhất, chi tiết sách Kết nối tri thức sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 2 Kết nối tri thức

Tổng hợp lý thuyết Toán 7 Chương 2

1. Số thập phân vô hạn tuần hoàn

• Số thập phân vô hạn tuần hoàn là số thập phân có phần thập phân lặp lại và phần lặp lại vô hạn.

• Chu kì của số thập phân vô hạn tuần hoàn là phần được lặp lại vô hạn lần.

• Số thập phân hữu hạn là số thập phân như 0,8; 1,25; …

2. Làm tròn số thập phân căn cứ vào độ chính xác cho trước

Khi làm tròn số đến một hàng nào đó, kết quả làm tròn có độ chính xác bằng một nửa đơn vị hàng làm tròn.

3. Số vô tỉ

• Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.

Tập hợp các số vô tỉ kí hiệu là $𝕀$.

4. Căn bậc hai số học

• Căn bậc hai số học của một số a không âm, kí hiệu là $\sqrt{a}$, là số x không âm sao cho

x²= a.

• Theo định nghĩa căn bậc hai số học ta có: ${\left(\sqrt{a}\right)}^2=\sqrt{a^2}=a$ với a ≥ 0.

5. Tính căn bậc hai số học bằng máy tính cầm tay

• Căn bậc hai số học của một số tự nhiên không chính phương luôn là một số vô tỉ.

• Cách tính căn bậc hai số học của một số a không âm bằng máy tính cầm tay

Phép tính: $\sqrt{a}$

Ấn các phím theo thứ tự: (a là một số không âm bất kì trên bàn phím máy tính)

6. Số thực và trục số thực

• Số hữu tỉ và số vô tỉ được gọi chung là số thực.

Tập hợp số thực được kí hiệu là .

• Mỗi số thực đều được biểu diễn bởi một điểm trên trục số. Ngược lại, mỗi điểm trên trục số đều biểu diễn một số thực.

7. Thứ tự trong tập hợp các số thực

• Các số thực đều được viết dưới dạng số thập phân (hữu hạn hoặc vô hạn). Vì thế có thể so sánh hai số thực bằng cách viết dưới dạng số thập phân.

• Cũng như các số hữu tỉ, ta có

Với hai số thực a và b bất kì ta luôn có a = b hoặc a < b hoặc a > b.

Cho ba số thực a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số thực, nếu a < b thì điểm a nằm trước điểm b. Các điểm nằm trước gốc O biểu diễn các số âm, các điểm nằm sau gốc O biểu diễn các số dương.

• x là số âm, ta viết: x < 0; x là số dương, ta viết: x > 0.

8. Giá trị tuyệt đối của một số thực

• Với số thực a tùy ý, ta có khoảng cách từ điểm a trên trục số đến gốc O là giá trị tuyệt đối của số a, kí hiệu là |a |

•Hai số đối nhau thì có giá trị tuyệt đối bằng nhau.

• Giá trị tuyệt đối của 0 là 0.

• Giá trị tuyệt đối của một số dương là chính nó.

• Giá trị tuyệt đối của một số âm là số đối của nó.

Bài tập tổng hợp Toán 7 Chương 2

Bài 1. Sử dụng chu kì, hãy viết gọn các số thập phân vô hạn tuần hoàn dưới đây:

a) 0,020202…

b) – 0,13999…

c) 5,3022121…

d) 0,1636363…

Hướng dẫn giải

a) Ta thấy số 0,020202… phần thập phân có chu kỳ là 02 nên 0,020202… = 0,(02)

b) Ta thấy số – 0,13999… phần thập phân có chu kỳ là 9 nên – 0,13999… = – 0,13(9)

c) Ta thấy số 5,3022121… phần thập phân có chu kỳ là 21 nên 5,3022121… = 5,302(21)

d) Ta thấy số 0,1636363… phần thập phân có chu kỳ là 63 nên 0,1636363… = 0,1(63)

Bài 2. Làm tròn các số 1,41421…; 1,9(81); 7,(35).

a) đến chữ số thập phân thứ ba;

b) với độ chính xác là 0,005.

Hướng dẫn giải

a) đến chữ số thập phân thứ ba

Số 1,41421… có chữ số sau chữ số thập phân thứ ba là 2 < 5.

Nên 1,41421… ≈ 1,414

Số 1,9(81) = 1,98181… có chữ số sau chữ số thập phân thứ ba là 8 > 5.

Nên 1,9(81) ≈ 1,982

Số 7,(35) = 7,3535… có chữ số sau chữ số thập phân thứ ba là 5 = 5.

Nên 7,(35) ≈ 7,354

b) với độ chính xác là 0,005 tức là làm tròn đến hàng phần trăm

Số 1,41421… có chữ số sau hàng phần trăm là 4 < 5.

Nên 1,41421… ≈ 1,41

Số 1,9(81) = 1,98181… có chữ số sau hàng phần trăm là 1 < 5.

Nên 1,9(81) ≈ 1,98

Số 7,(35) = 7,3535… có chữ số sau hàng phần trăm là 3 < 5.

Nên 7,(35) ≈ 7,35.

Bài 3. Điền kí hiệu ($\in ;\notin$) thích hợp vào chỗ chấm:

a) 2,5 … $𝕀$

b) $-\frac{4}{3}$ … $𝕀$

c) 0 … $𝕀$

d) $\sqrt{6}$ … $𝕀$

e) $\sqrt{4}$ … $𝕀$

Hướng dẫn giải

a) Vì 2,5 là số thập phân hữu hạn nên 2,5 $\notin 𝕀$;

b) Vì $-\frac{4}{3}=-1,\left(3\right)$ là số thập phân vô hạn tuần hoàn nên $-\frac{4}{3}$ $\notin 𝕀$;

c) 0 $\notin 𝕀$;

d) Vì 6 không là số chính phương nên $\sqrt{6}$ $\in 𝕀$;

e) Vì 2² = 4 và 2 > 0 nên $\sqrt{4}=2$ nên $\notin 𝕀$.

Bài 5. Để lát một mảnh sân có diện tích 240 m² người ta cần 800 viên gạch hoa hình vuông. Tính độ dài cạnh của mỗi viên gạch hoa theo đơn vị đề-xi-mét (làm tròn kết quả đến hàng phần mười). Coi các mạch ghép là không đáng kể.

Hướng dẫn giải

Đổi 240 m² = 24000 dm²

Diện tích của mỗi viên gạch hoa là: 24000 : 800 = 30 (dm²)

Vì $30={\left(\sqrt{30}\right)}^2$ nên độ dài cạnh của viên gạch hoa là: $\sqrt{30}$ dm

Sử dụng máy tính cầm tay ta tính được $\sqrt{30}$ ≈ 5,477225575.

Làm tròn kết quả đến hàng phần mười ta được độ dài cạnh viên gạch hoa là 5,5 dm.

Bài 2. So sánh:

a) 28,03 và 28,0(23)

b) $\sqrt{5}$ và $\sqrt{7}$

c) 4 và $\sqrt{10}$

d) –19,11 và –19,(1)

e) –2 và $-\sqrt{3}$

f) $\sqrt{2+3+4}$ và 3

g) |5| và |3|

Hướng dẫn giải

a) Vì 3 > 2 nên 28,03 > 28,02323… nên 28,03 > 28,0(23)

b) Vì $5<7$ nên $\sqrt{5}$ < $\sqrt{7}$

c) Vì 4 > 0 nên $4=\sqrt{4^2}=\sqrt{16}$

Mà 16 > 10 nên $\sqrt{16}>\sqrt{10}$.

Do đó: $4>\sqrt{10}$

d) Vì 0 < 1 nên 19,110 < 19,111 nên –19,11 > –19,(1)

e) Vì 2 > 0 nên $2=\sqrt{2^2}=\sqrt{4}$. Mà 4 > 3 nên $\sqrt{4}>\sqrt{3}$.

Do đó $2>\sqrt{3}$. Vậy –2 < $-\sqrt{3}$.

f) $\sqrt{2+3+4}=\sqrt{9}=\sqrt{3^2}=3$ nên $\sqrt{2+3+4}=3$.

g) $\left|5\right|=5$ (vì $-5<0$) và $\left|3\right|=3$ (vì 3 > 0). Mà 5 > 3 nên $|-5|$ > $\left|3\right|$

Bài 6. Tìm x, biết:

a) $\left|x\right|=0$

b) $\left|x\right|=\frac{1}{3}$

c) $\left|x\right|=0,46$

d) $|x-1|=2$

e) $\left|x\right|<3$ ($x\in \mathbb{Z}$)

Hướng dẫn giải

a) $\left|x\right|=0$ thì $x=0$

b) $\left|x\right|=\frac{1}{3}$ thì $x=\frac{1}{3}$ hoặc $x=-\frac{1}{3}$

c) $\left|x\right|=0,46$ thì x = 0,46 hoặc x = – 0,46

d) $|x-1|=2$

Trường hợp 1:

$x-1=2$

x = 2 + 1

x = 3

Trường hợp 2:

$x-1=-2$

$x=-2+1$

$x=-1$

Vậy $x=3$ hoặc $x=-1$

e) $\left|x\right|<3$ ($x\in \mathbb{Z}$)

$-3<x<3$

$x\in \left(-2;-1;0;1;2\right)$

Bài 7.Từ các số là bình phương của 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:

a) 9;  b) 16;

c) 81;  d) 121.

Hướng dẫn giải:

Theo đề bài, ta tính bình phương của 12 số tự nhiên đầu tiên và thấy rằng:

3² = 9; 4² = 16; 9² = 81; 11² = 121.

a) Vì 3² = 9 và 3 > 0 nên $\sqrt{9}=3.$

Vậy căn bậc hai số học của 9 là 3.

b) Vì 4² = 16 và 4 > 0 nên $\sqrt{16}=4.$

Vậy căn bậc hai số học của 16 là 4.

c) Vì 9² = 81 và 9 > 0 nên $\sqrt{81}=9.$

Vậy căn bậc hai số học của 81 là 9.

d) Vì 11² = 121 và 11 > 0 nên $\sqrt{121}=11.$

Vậy căn bậc hai số học của 121 là 11.

Bài 8.Cho tập hợp A = {7,1; –2,(61); 0; 5,14; $\frac{4}{7};\sqrt{15};-\sqrt{81}$}.

Viết tập hợp A’ gồm các phần tử là số đối củ các phần tử ở tập hợp A.

Hướng dẫn giải:

Tập hợp A = {7,1; –2,(61); 0; 5,14; $\frac{4}{7};\sqrt{15};-\sqrt{81}$}.

Số đối của 7,1 là –7,1.

Số đối của –2,(61) là 2,61.

Số đối của 0 là 0.

Số đối của 5,14 là –5,14.

Số đối của $\frac{4}{7}$ là $-\frac{4}{7}.$

Số đối của $\sqrt{15}$ là $-\sqrt{15}.$

Số đối của $-\sqrt{81}$ là $\sqrt{81}.$

Vậy tập hợp các số đối của các số thuộc tập hợp A là:

$A^{\text{'}}=\left(-7,1;2,\left(61\right);0;-5,14;-\frac{4}{7};-\sqrt{15};\sqrt{81}\right).$

Học tốt Toán 7 Chương 2

Các bài học để học tốt Chương 2 Toán lớp 7 hay khác:

• Giải sgk Toán 7 Ôn tập chương 2

• Giải sbt Toán 7 Ôn tập chương 2