Tổng hợp lý thuyết Toán 7 Chương 1 Kết nối tri thức

---

Với tổng hợp lý thuyết Toán lớp 7 Chương 1: Số hữu tỉ hay nhất, chi tiết sách Kết nối tri thức sẽ giúp học sinh lớp 7 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 7.

Tổng hợp lý thuyết Toán 7 Chương 1 Kết nối tri thức

Tổng hợp lý thuyết Toán 7 Chương 1

1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số

• Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}$ với a, b ∈ $\mathbb{Z}$, b ≠ 0.

Tập hợp các số hữu tỉ được kí hiệu là $\mathbb{Q}$.

• Cách biểu diễn số hữu tỉ $\frac{a}{b}$ trên trục số:

 + Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.

 + Điểm biểu diễn số hữu tỉ $\frac{a}{b}$ cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).

Ví dụ:

+  Các số – 7; 0,3; – 2$\frac{3}{4}$ là các số hữu tỉ vì – 7 = $\frac{-7}{1}$; 0,3 = $\frac{3}{10}$; – 2$\frac{3}{4}$ = $\frac{-11}{4}$.

+ Biểu diễn số hữu tỉ $\frac{3}{2}$ trên trục số ta làm như sau:

    Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).

    Số hữu tỉ $\frac{3}{2}$ được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)

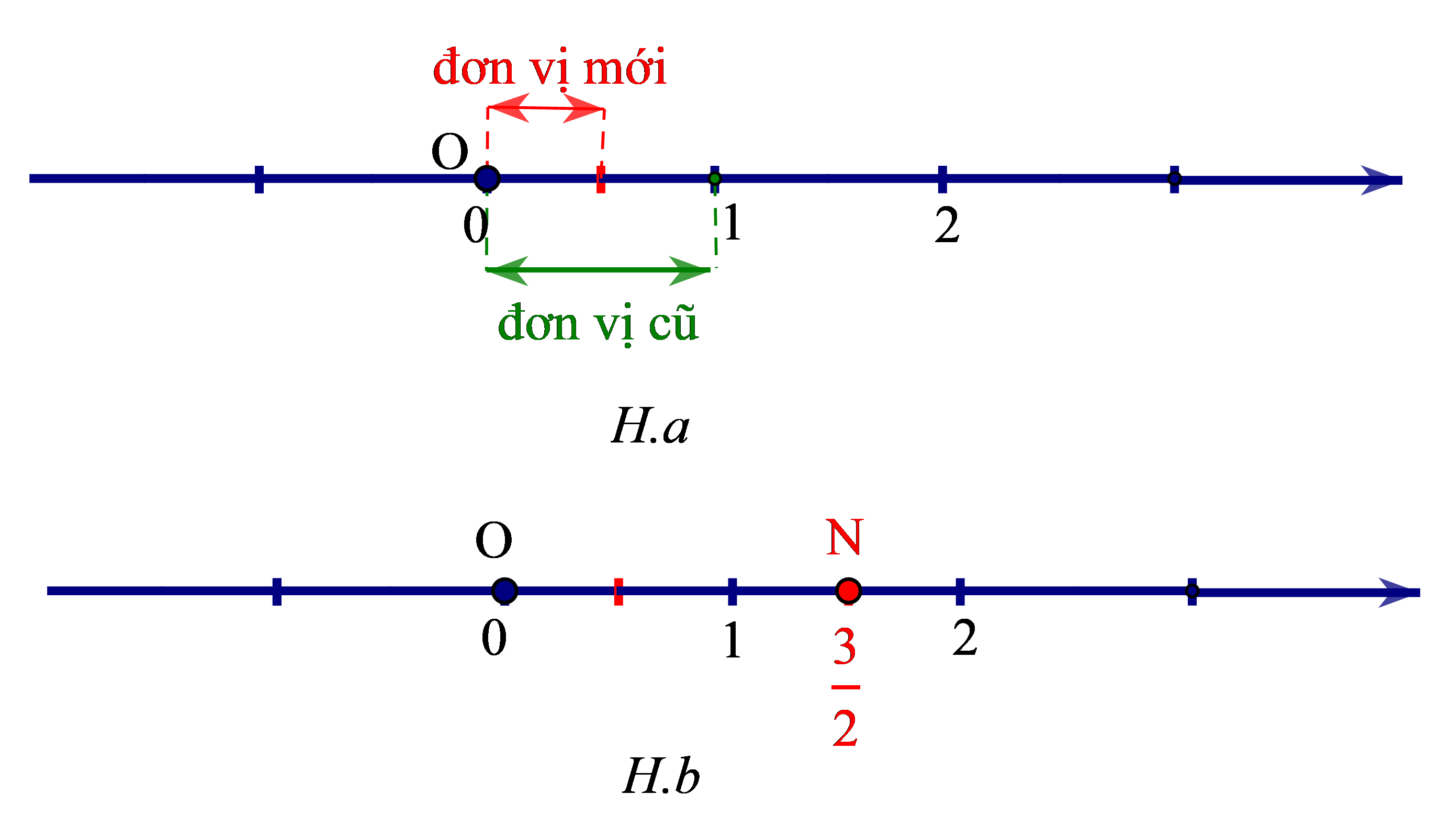
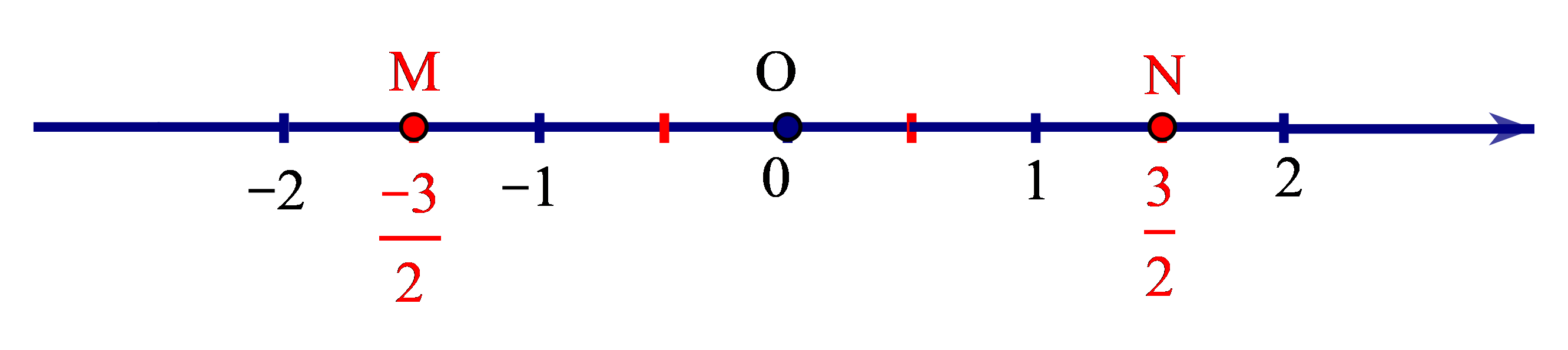
+ Số đối của số hữu tỉ $\frac{3}{2}$ là số hữu tỉ $-\frac{3}{2}$ được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.

Chú ý:

• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.

• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.

• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.

2. Thứ tự trong tập hợp các số hữu tỉ

• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Ví dụ:

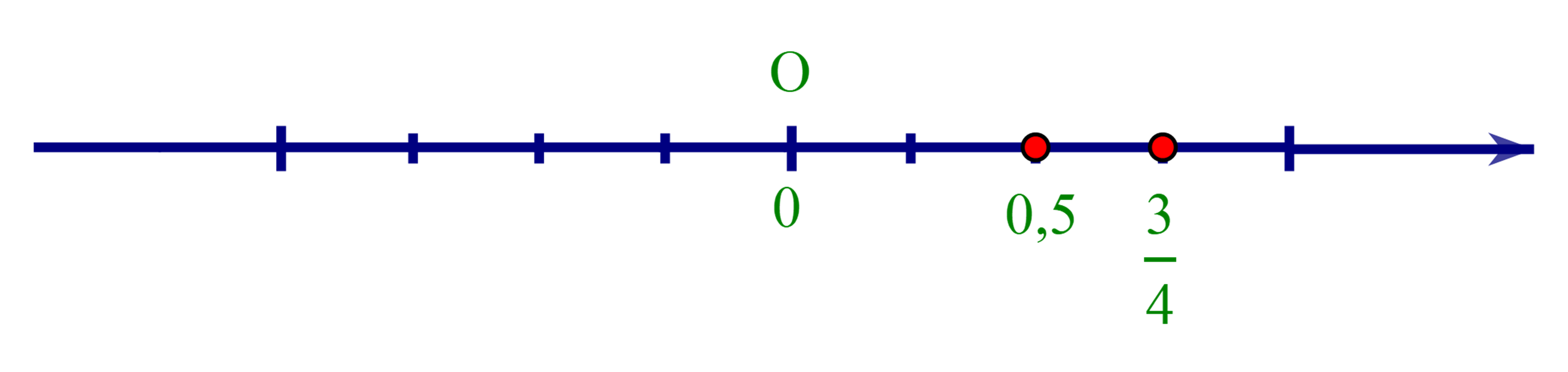
+ So sánh 0,5 và $\frac{3}{4}$ ta làm như sau: 0,5 = $\frac{5}{10}=\frac{2}{4}$ và $\frac{3}{4}$. Vì $\frac{2}{4}$ < $\frac{3}{4}$ nên 0,5 < $\frac{3}{4}$.

+ 0,5 < $\frac{3}{4}$ nên 0,5 nằm trước $\frac{3}{4}$ trên trục số.

+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ $\frac{5}{6}$ và $\frac{6}{5}$ như sau:

Vì $\frac{5}{6}$ < 1 và 1 < $\frac{6}{5}$ nên $\frac{5}{6}$ < $\frac{6}{5}$.

Chú ý:

• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

3. Cộng và trừ hai số hữu tỉ

Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

Ví dụ:

+  Tính: $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$

Hướng dẫn giải

 $\frac{2}{-3}+\frac{-5}{6}+\frac{1}{3}+1\frac{1}{6}$

$=\frac{-2}{3}+\frac{-5}{6}+\frac{1}{3}+\frac{7}{6}$             (Viết số hữu tỉ dưới dạng phân số có mẫu dương)

$=\frac{-2}{3}+\frac{1}{3}+\frac{-5}{6}+\frac{7}{6}$             (Tính chất giao hoán)

$=\left(\frac{-2}{3}+\frac{1}{3}\right)+\left(\frac{-5}{6}+\frac{7}{6}\right)$      (Tính chất kết hợp)

$=\frac{-1}{3}+\frac{2}{6}$

$=\frac{-1}{3}+\frac{1}{3}=0$                       (Tổng hai số đối nhau bằng 0)

+  Tính: $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$

Hướng dẫn giải

 $\frac{31}{3}-\frac{1}{2}-\left(\frac{2}{3}-\frac{1}{2}\right)$

$=\frac{31}{3}-\frac{1}{2}-\frac{2}{3}+\frac{1}{2}$                    (Quy tắc bỏ dấu ngoặc có dấu “–” đằng trước)

$=\left(\frac{31}{3}-\frac{2}{3}\right)+\left(-\frac{1}{2}+\frac{1}{2}\right)$         (Quy tắc đặt dấu ngoặc có dấu “+” đằng trước)

$=\frac{29}{3}+0=\frac{29}{3}$                       (Cộng với số 0)

Chú ý:

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc cộng và trừ đối với số thập phân.

• Trong phép cộng trừ với số hữu tỉ $\mathbb{Q}$, ta có thể áp dụng các tính chất giao hoán, kết hợp, quy tắc dấu ngoặc như trong phép cộng trừ với số nguyên $\mathbb{Z}$.

• Đối với một tổng trong $\mathbb{Q}$, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong $\mathbb{Z}$.

• Hai số đối nhau luôn có tổng bằng 0:

a + (– a) = 0.

4. Nhân và chia hai số hữu tỉ

• Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Ví dụ:

+  Tính $\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$

Hướng dẫn giải

$\frac{23}{3}\cdot \frac{6}{46}\cdot \left(-\frac{9}{10}\right)$

$=\frac{23}{3}\cdot \frac{3}{23}\cdot \left(-\frac{9}{10}\right)$

$=1\cdot \left(-\frac{9}{10}\right)=-\frac{9}{10}$                (Nhân với số 1)

+  Tính $-\frac{7}{6}:1\frac{5}{7}$

Hướng dẫn giải

$-\frac{7}{6}:1\frac{5}{7}$

$=-\frac{7}{6}:\frac{12}{7}$

$=-\frac{7}{6}\cdot \frac{7}{12}=-\frac{49}{72}$

+  Tính hợp lí: $\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$

Hướng dẫn giải

$\frac{7}{6}\cdot 3\frac{1}{4}+\frac{7}{6}\cdot \left(-0,25\right)$

$=\frac{7}{6}\cdot \left[3\frac{1}{4}+\left(-0,25\right)\right]$

$=\frac{7}{6}\cdot \left(\frac{13}{4}+\frac{-1}{4}\right)$

$=\frac{7}{6}\cdot \frac{12}{4}=\frac{7}{2}$

Chú ý:

• Phép nhân các số hữu tỉ cũng có các tính chất của phép nhân phân số.

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.

Ví dụ: 1,25 . (– 4,6) = – (1,25 . 4,6) = – 5,75.

5. Lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1)

$x^n=\underset{nthừasố}{\underbrace{x\cdot x\cdot x\cdot \mathrm{...}\cdot x}}$ (x $\in \mathbb{Q}$, n $\in \mathbb{N}$, n >1)

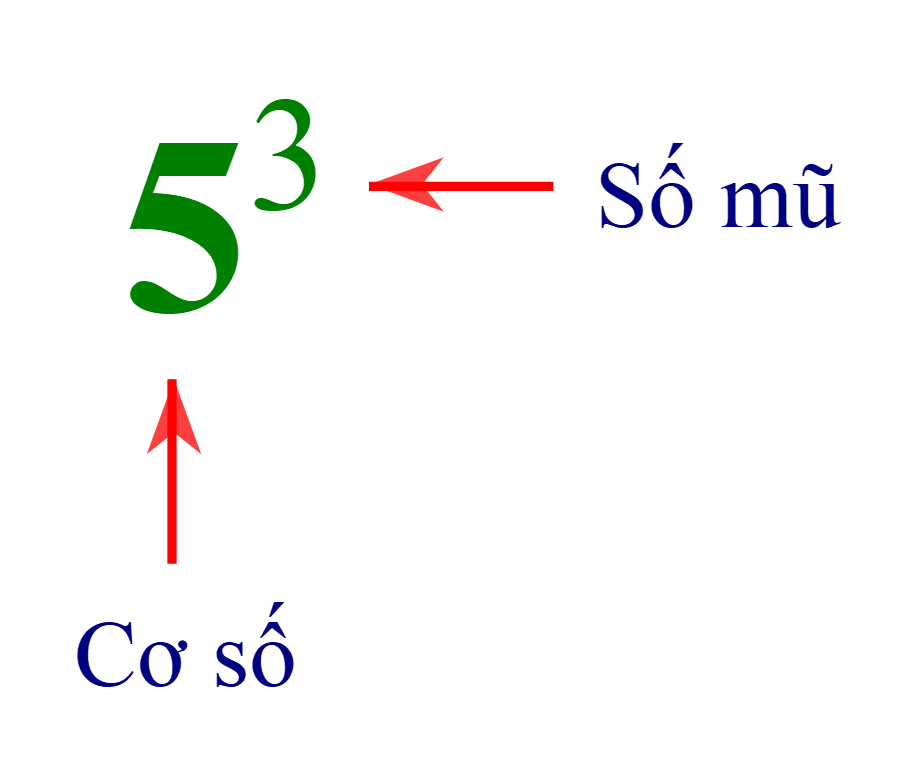
xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.

x gọi là cơ số, n gọi là số mũ.

Quy ước: x⁰ = 1 (x ≠ 0); x¹ = x.

Ví dụ:

+ 5³ đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.

+ Tính ${\left(\frac{-1}{3}\right)}^4$

${\left(\frac{-1}{3}\right)}^4=\frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}\cdot \frac{-1}{3}=\frac{\left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)\cdot \left(-1\right)}{3\cdot 3\cdot 3\cdot 3}=\frac{1}{81}$

+ Tính và so sánh: $\frac{{12}^2}{6^2}$và ${\left(-\frac{12}{6}\right)}^2$

$\frac{{12}^2}{6^2}=\frac{144}{36}=4$và ${\left(-\frac{12}{6}\right)}^2={\left(-2\right)}^2=4$nên $\frac{{12}^2}{6^2}={\left(-\frac{12}{6}\right)}^2$

Chú ý:

• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.

${\left(x\cdot y\right)}^n=x^n\cdot y^n$; ${\left(\frac{x}{y}\right)}^n=\frac{x^n}{y^n}$ (y ≠ 0).

Ví dụ:

${\left(\frac{3}{4}\right)}^{15}{.4}^{15}={\left(\frac{3}{4}.4\right)}^{15}=3^{15}$;

25³ : 5³ = ${\left(\frac{25}{5}\right)}^3=5^3=125$ .

6. Nhân và chia hai lũy thừa cùng cơ số

• Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

$x^m\cdot x^n=x^{m+n}$

• Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.

$x^m:x^n=x^{m-n}$(x ≠ 0, m ≥ n)

Ví dụ:

+ Tính ${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5$

${\left(\frac{2}{3}\right)}^2.{\left(\frac{2}{3}\right)}^5={\left(\frac{2}{3}\right)}^{2+5}={\left(\frac{2}{3}\right)}^7=\frac{128}{2187}$

+ Tính ${\left(-9\right)}^5:{\left(-9\right)}^4$

${\left(-9\right)}^5:{\left(-9\right)}^4={\left(-9\right)}^{5-4}={\left(-9\right)}^1=-9$.

7. Lũy thừa của lũy thừa

• Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

${\left(x^m\right)}^n=x^{m\cdot n}$

Ví dụ:

+ Tính ${\left({\left(-3\right)}^5\right)}^7$

${\left({\left(-3\right)}^5\right)}^7={\left(-3\right)}^{5\cdot 7}={\left(-3\right)}^{35}$.

Mở rộng

• Lũy thừa với số mũ nguyên âm của một số khác 0.

$x^{-n}=\frac{1}{x^n}$với n là số nguyên dương, x ≠ 0.

Ví dụ: $\frac{1}{100}=\frac{1}{{10}^2}={10}^{-2}$

8. Thứ tự thực hiện các phép tính

• Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia ta thực hiện các phép tính theo thứ tự từ trái sang phải.

• Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:

• Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.

$\left(\right)\to \left[\right]\to \left\{\right\}$

Ví dụ:

+ Tính giá trị của biểu thức: 1,5 – 2³ + 7,5 : 3

1,5 – 2³ + 7,5 : 3

= 1,5 – 8 + 2,5 (Thực hiện lũy thừa; nhân chia trước)

= – 6,5 + 2,5 = – 4

+ Tính giá trị của biểu thức: $\frac{3}{2}:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac{7}{4}\cdot \left(\frac{1}{14}-\frac{2}{7}\right)$

$\frac{3}{2}:\left(\frac{1}{11}-\frac{5}{22}\right)+\frac{7}{4}\cdot \left(\frac{1}{14}-\frac{2}{7}\right)$

$=\frac{3}{2}:\left(-\frac{3}{22}\right)+\frac{7}{4}\cdot \left(-\frac{3}{14}\right)$ (Thực hiện trong ngoặc trước)

$=\frac{3}{2}\cdot \left(-\frac{22}{3}\right)+\left(-\frac{3}{8}\right)$ (Thực hiện nhân chia trước)

$=\left(-11\right)+\left(-\frac{3}{8}\right)=-\frac{91}{8}$.

9. Quy tắc chuyển vế

• Đẳng thức có dạng A = B. Trong đó A là vế trái; B là vế phải của đẳng thức.

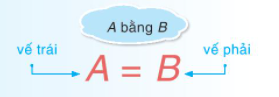
Ví dụ: 4,1 + x = 2,3 là một đẳng thức, trong đó 4,1 + x là vế trái, 2,3 là vế phải.

• Khi biến đổi các đẳng thức, ta thường áp dụng các tính chất sau:

Nếu a = b thì:b = a;a + c = b + c.

• Quy tắc chuyển vế:Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu “+”.

Nếu a + b = c thì a = c – b;

Nếu a – b = c thì a = c + b.

Ví dụ:

+ Tìm x, biết: $x+\frac{1}{3}=-\frac{5}{7}$

$x+\frac{1}{3}=-\frac{5}{7}$

$x=-\frac{15}{21}-\frac{7}{21}$(Quy tắc chuyển vế)

$x=-\frac{15}{21}-\frac{7}{21}$

$x=-\frac{22}{21}$

Vậy $x=-\frac{22}{21}$.

+Tìm x, biết: $x-\frac{5}{4}=\frac{9}{8}$

$x-\frac{5}{4}=\frac{9}{8}$

$x=\frac{9}{8}+\frac{5}{4}$(Quy tắc chuyển vế)

$x=\frac{9}{8}+\frac{10}{8}$

$x=\frac{19}{8}$

Vậy $x=\frac{19}{8}$.

Bài tập tổng hợp Toán 7 Chương 1

Bài 1. Điền kí hiệu (∈, ∉) thích hợp vào chỗ chấm:

a) 0,25 … $\mathbb{Q}$ ;

b) $-\frac{5}{7}$ … $\mathbb{Q}$ ;

c) 0 … $\mathbb{Q}$ ;

d) $3\frac{1}{8}$ … $\mathbb{Q}$ .

Hướng dẫn giải

a) Vì 0,25 = $\frac{1}{4}$ nên 0,25 $\in$ $\mathbb{Q}$

b) $-\frac{5}{7}$ $\in$ $\mathbb{Q}$

c) Vì 0 = $\frac{0}{1}$ nên 0 $\in$ $\mathbb{Q}$

d) Vì $3\frac{1}{8}$ = $\frac{25}{8}$ nên $3\frac{1}{8}$ $\in$ $\mathbb{Q}$ .

Bài 2. Cho trục số sau:

a) Các điểm A, B, C, D biểu diễn những số hữu tỉ nào?

b) Tìm số đối của các số hữu tỉ trên và biểu diễn chúng trên trục số.

Hướng dẫn giải

a) Ta thấy đoạn thẳng đơn vị cũ (ví dụ đoạn từ 0 đến 1) được chia thành 5 phần bằng nhau nên đoạn đơn vị mới bằng $\frac{1}{5}$ đơn vị cũ. Do đó:

Điểm A nằm trước gốc O và cách gốc O một khoảng bằng 7 đơn vị nên nó biểu diễn số hữu tỉ $-\frac{7}{5}$ .

Tương tự, ta có được:

Điểm B biểu diễn số hữu tỉ $-\frac{2}{5}$ .

Điểm C biểu diễn số hữu tỉ $\frac{4}{5}$ .

Điểm D biểu diễn số hữu tỉ $\frac{9}{5}$ .

b) Số đối của $-\frac{7}{5}$ là $-\left(-\frac{7}{5}\right)=\frac{7}{5}$

Số đối của $-\frac{2}{5}$ là $-\left(-\frac{2}{5}\right)=\frac{2}{5}$

Số đối của $\frac{4}{5}$ là $-\frac{4}{5}$

Số đối của $\frac{9}{5}$ là $-\frac{9}{5}$

Biểu diễn trên trục số:

Bài 3. So sánh:

a) – 1,25 và – 1,125;

b) $0,8$ và $\frac{8}{15}$ ;

c) $-\frac{2}{19}$ và $-\frac{10}{19}$ ;

d) $2\frac{2}{3}$ và $\frac{17}{6}$ ;

e) $\frac{1}{2022}$ và $\frac{1}{2023}$ ;

f) – 5,6 và $\frac{1}{2}$ ;

g) $\frac{7}{9}$ và 1,5.

Hướng dẫn giải

a) Có 1,25 > 1,125 nên – 1,25 < – 1,125

b) Có $0,8$ = $\frac{8}{10}=\frac{4}{5}=\frac{12}{15}$ , vì $\frac{12}{15}$ > $\frac{8}{15}$ . Nên 0,8 > $\frac{8}{15}$

c) Có $\frac{2}{19}$ < $\frac{10}{19}$ nên $-\frac{2}{19}$ > $-\frac{10}{19}$

d) Có $2\frac{2}{3}=\frac{8}{3}=\frac{16}{6}$ , vì $\frac{16}{6}$ < $\frac{17}{6}$ . Nên $2\frac{2}{3}$ < $\frac{17}{6}$

e) $\frac{1}{2022}$ > $\frac{1}{2023}$

f) Có – 5,6 < 0 và $\frac{1}{2}$ > 0. Nên – 5,6 < $\frac{1}{2}$

g) Có $\frac{7}{9}$ < 1 và 1,5 > 1. Nên $\frac{7}{9}$ < 1,5.

Bài 4. Tính:

a)  $\frac{-8}{18}+\frac{15}{27}$;

b)  $3,5-\left(-\frac{2}{7}\right)$;

c)  $-0,25\cdot \left(-0,4\right)$;

d)  $-6:3\frac{1}{5}$.

Hướng dẫn giải

a) $\frac{-8}{18}+\frac{15}{27}=\frac{-4}{9}+\frac{5}{9}=\frac{1}{9}$ 

b) $3,5-\left(-\frac{2}{7}\right)=\frac{7}{2}+\frac{2}{7}=\frac{49}{14}+\frac{4}{14}=\frac{53}{14}$ 

c) $-0,25\cdot \left(-0,4\right)=0,25\cdot 0,4=0,1$ 

d)  $-6:3\frac{1}{5}=-6:\frac{16}{5}=-6\cdot \frac{5}{16}=\frac{-15}{8}$.

Bài 5. Tính giá trị của các biểu thức sau:

a)  $\left(7+3\frac{1}{4}-\frac{3}{5}\right)+\left(0,4-5\right)-\left(4\frac{1}{4}-1\right)$;

b)  $\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]$;

c)  $\left(9-\frac{1}{2}-\frac{3}{4}\right):\left(7-\frac{1}{4}-\frac{5}{8}\right)$;

d)  $3-\frac{1-\frac{1}{7}}{1+\frac{1}{7}}$.

Hướng dẫn giải

a) $\left(7+3\frac{1}{4}-\frac{3}{5}\right)+\left(0,4-5\right)-\left(4\frac{1}{4}-1\right)$  

$=7+3\frac{1}{4}-\frac{3}{5}+0,4-5-4\frac{1}{4}+1$

$=\left(7-5+1\right)+\left(3\frac{1}{4}-4\frac{1}{4}\right)+\left(-\frac{3}{5}+0,4\right)$

$=3+\left(-1\right)+\left(-0,6+0,4\right)$

$=2+\left(-0,2\right)=1,8$

b) $\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{1}{2}+\frac{3}{8}\right)\right]$ 

$=\frac{2}{3}-\left[\left(-\frac{7}{4}\right)-\left(\frac{4}{8}+\frac{3}{8}\right)\right]$

$=\frac{2}{3}-\left[\left(-\frac{14}{8}\right)-\frac{7}{8}\right]$

$=\frac{2}{3}-\left(-\frac{21}{8}\right)$

$=\frac{2}{3}+\frac{21}{8}$

$=\frac{16}{24}+\frac{63}{24}=\frac{79}{24}$

c)  $\left(9-\frac{1}{2}-\frac{3}{4}\right):\left(7-\frac{1}{4}-\frac{5}{8}\right)$

$=\left(\frac{36}{4}-\frac{2}{4}-\frac{3}{4}\right):\left(\frac{56}{8}-\frac{2}{8}-\frac{5}{8}\right)$

$=\frac{31}{4}:\frac{49}{8}=\frac{31}{4}\cdot \frac{8}{49}=\frac{62}{49}$

d) $3-\frac{1-\frac{1}{7}}{1+\frac{1}{7}}=3-\left(1-\frac{1}{7}\right):\left(1+\frac{1}{7}\right)$

$=3-\frac{6}{7}:\frac{8}{7}=3-\frac{6}{7}\cdot \frac{7}{8}$

$=3-\frac{3}{4}=\frac{12}{4}-\frac{3}{4}=\frac{9}{4}$

Bài 6. Tính một cách hợp lí.

a)  $3\frac{3}{4}+\left(-0,7\right)+\frac{5}{4}+\left(-4,3\right)$;

b)  $2\frac{3}{5}\cdot \left(-2022\right)+0,45\cdot 94-2,6\cdot \left(-2022\right)+0,55\cdot 94$;

c)  $\left(6-\frac{5}{3}+\frac{1}{2}\right)-\left(3+\frac{2}{3}-\frac{3}{2}\right)-\left(5+\frac{5}{2}-\frac{7}{3}\right)$;

d)  $-2,4\cdot \frac{17}{4}+\frac{12}{7}\cdot \frac{-85}{6}-2,4\cdot \left(-5\frac{5}{4}\right)-\frac{12}{7}\cdot \frac{-71}{6}$.

Hướng dẫn giải

a) $3\frac{3}{4}+\left(-0,7\right)+\frac{5}{4}+\left(-4,3\right)$ 

$=3,75+\left(-0,7\right)+1,25+\left(-4,3\right)$

$=\left(3,75+1,25\right)+\left[\left(-0,7\right)+\left(-4,3\right)\right]$

$=5+\left(-5\right)=0$

b)  $2\frac{3}{5}\cdot \left(-2022\right)+0,45\cdot 94-2,6\cdot \left(-2022\right)+0,55\cdot 94$

$=2,6\cdot \left(-2022\right)-2,6\cdot \left(-2022\right)+\left(0,45+0,55\right)\cdot 94$

$=\left(2,6-2,6\right)\cdot \left(-2022\right)+1\cdot 94$

$=0\cdot \left(-2022\right)+94$

$=0+94=94$

c) $\left(6-\frac{5}{3}+\frac{1}{2}\right)-\left(3+\frac{2}{3}-\frac{3}{2}\right)-\left(5+\frac{5}{2}-\frac{7}{3}\right)$ 

$=6-\frac{5}{3}+\frac{1}{2}-3-\frac{2}{3}+\frac{3}{2}-5-\frac{5}{2}+\frac{7}{3}$

$=\left(6-3-5\right)-\left(\frac{5}{3}+\frac{2}{3}-\frac{7}{3}\right)+\left(\frac{1}{2}+\frac{3}{2}-\frac{5}{2}\right)$

$=-2-0+\left(-\frac{1}{2}\right)$

 $=\frac{-4}{2}+\left(\frac{-1}{2}\right)=\frac{-5}{2}$.

d) $-2,4\cdot \frac{17}{4}+\frac{12}{7}\cdot \frac{-85}{6}-2,4\cdot \left(-5\frac{5}{4}\right)-\frac{12}{7}\cdot \frac{-71}{6}$ 

$=-2,4\cdot \left[\frac{17}{4}+\left(-5\frac{5}{4}\right)\right]+\frac{12}{7}\cdot \left(\frac{-85}{6}-\frac{-71}{6}\right)$

$=-2,4\cdot \left(\frac{17}{4}+\frac{-25}{4}\right)+\frac{12}{7}\cdot \left(\frac{-85}{6}+\frac{71}{6}\right)$

$=-2,4\cdot \left(\frac{-8}{4}\right)+\frac{12}{7}\cdot \left(\frac{-14}{6}\right)$

$=-2,4\cdot \left(-2\right)+\frac{12}{7}\cdot \left(\frac{-7}{3}\right)$

 $=4,8+\left(-4\right)=0,8$.

Bài 7. Tính:

a) ${\left(-2\frac{1}{2}\right)}^3$;

b) ${\left(-2\frac{1}{2}\right)}^4$;

c) ${\left(1+\frac{1}{2}-\frac{1}{4}\right)}^2\cdot {2022}^0$;

d) $2:{\left(\frac{1}{2}-\frac{2}{3}\right)}^3$.

Hướng dẫn giải

a) ${\left(-2\frac{1}{2}\right)}^3$$={\left(-\frac{5}{2}\right)}^3=-\frac{125}{8}$

b) ${\left(-2\frac{1}{2}\right)}^4={\left(-\frac{5}{2}\right)}^4=\frac{625}{16}$

c) ${\left(1+\frac{1}{2}-\frac{1}{4}\right)}^2\cdot {2022}^0$$={\left(\frac{5}{4}\right)}^2\cdot 1=\frac{25}{16}$

d) $2:{\left(\frac{1}{2}-\frac{2}{3}\right)}^3$

$=2:{\left(\frac{3}{6}-\frac{4}{6}\right)}^3=2:{\left(-\frac{1}{6}\right)}^3=2:\frac{-1}{216}=2\cdot \left(-216\right)=-432$.

Bài 8. Tìm x, biết:

a) $x:{\left(-\frac{1}{2}\right)}^3=-\frac{1}{2}$;

b) ${\left(\frac{3}{4}\right)}^5\cdot x={\left(\frac{3}{4}\right)}^7$;

c) $\frac{343}{125}={\left(\frac{7}{5}\right)}^x$;

d) ${\left(-\frac{1}{3}\right)}^x=-\frac{1}{243}$.

Hướng dẫn giải

a) $x:{\left(-\frac{1}{2}\right)}^3=-\frac{1}{2}$

$x=-\frac{1}{2}\cdot {\left(-\frac{1}{2}\right)}^3$

$x={\left(-\frac{1}{2}\right)}^{3+1}$

$x={\left(-\frac{1}{2}\right)}^4=\frac{1}{16}$.

 Vậy $x=\frac{1}{16}$.

b) ${\left(\frac{3}{4}\right)}^5\cdot x={\left(\frac{3}{4}\right)}^7$

$x={\left(\frac{3}{4}\right)}^7:{\left(\frac{3}{4}\right)}^5$

$x={\left(\frac{3}{4}\right)}^{7-5}$

$x={\left(\frac{3}{4}\right)}^2=\frac{9}{16}$.

Vậy $x=\frac{9}{16}$.

c) $\frac{343}{125}={\left(\frac{7}{5}\right)}^x$

${\left(\frac{7}{5}\right)}^3={\left(\frac{7}{5}\right)}^x$

$x=3$.

Vậy x = 3.

d) ${\left(-\frac{1}{3}\right)}^x=-\frac{1}{243}$

${\left(-\frac{1}{3}\right)}^x={\left(-\frac{1}{3}\right)}^5$

$x=5$.

Vậy x = 5.

Bài 9. Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ.

a) 25⁴ . 2⁸;

b) 27² : 25³;

c) 15⁸ . 9⁴;

d) (–27)⁵ : 32³.

Hướng dẫn giải

a) 25⁴ . 2⁸$={\left(5^2\right)}^4\cdot 2^8=5^{2\cdot 4}\cdot 2^8=5^8\cdot 2^8={\left(5\cdot 2\right)}^8={10}^8$

b) 27² : 25³ $={\left(3^3\right)}^2:{\left(5^2\right)}^3=3^6:5^6={\left(\frac{3}{5}\right)}^6$

c) 15⁸ . 9⁴$={15}^8\cdot {\left(3^2\right)}^4={15}^8\cdot 3^8={\left(15\cdot 3\right)}^8={45}^8$

d) (–27)⁵ : 32³ = ${\left[{\left(-3\right)}^3\right]}^5:{\left(2^5\right)}^3={\left(-3\right)}^{15}:2^{15}={\left(\frac{-3}{2}\right)}^{15}$.

Bài 10. Tính:

a) $\frac{4^2\cdot 4^3}{2^{10}}$;

b) $\frac{5^4\cdot {20}^4}{{25}^5\cdot 4^5}$;

c) $\frac{2^7\cdot 9^3}{6^5\cdot 8^2}$;

d) $\frac{6^3+3\cdot 6^2+3^3}{-13}$.

Hướng dẫn giải

a) $\frac{4^2\cdot 4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{{\left(2^2\right)}^5}{2^{10}}=\frac{2^{10}}{2^{10}}=1$

b) $\frac{5^4\cdot {20}^4}{{25}^5\cdot 4^5}=\frac{{\left(5\cdot 20\right)}^4}{{\left(25\cdot 4\right)}^5}=\frac{{100}^4}{{100}^5}=\frac{1}{100}$

c) $\frac{2^7\cdot 9^3}{6^5\cdot 8^2}=\frac{2^7\cdot {\left(3^2\right)}^3}{{\left(2\cdot 3\right)}^5\cdot {\left(2^3\right)}^2}=\frac{2^7\cdot 3^6}{2^5\cdot 3^5\cdot 2^6}=\frac{2^7\cdot 3^6}{2^{11}\cdot 3^5}=\frac{3}{2^4}=\frac{3}{16}$

d) $\frac{6^3+3\cdot 6^2+3^3}{-13}=\frac{3^3\cdot 2^3+3\cdot 3^2\cdot 2^2+3^3}{-13}=\frac{3^3\cdot \left(2^3+2^2+1\right)}{-13}=\frac{27\cdot 13}{-13}=-27$.

Bài 11. Tìm x, biết:

a) $x+0,5=-\frac{2}{3}$;

b) $x-\left(-\frac{2}{5}\right)=\frac{5}{7}$;

c) $\frac{5}{4}-6x=\frac{7}{12}$;

d) $3-2x-\left(\frac{5}{4}-\frac{7}{5}\right)=\frac{9}{20}$.

Hướng dẫn giải

a) $x+0,5=-\frac{2}{3}$

$x=-\frac{2}{3}-0,5$

$x=-\frac{2}{3}-\frac{1}{2}$

$x=-\frac{4}{6}-\frac{3}{6}$

$x=-\frac{7}{6}$

Vậy $x=-\frac{7}{6}$.

b) $x-\left(-\frac{2}{5}\right)=\frac{5}{7}$

$x=\frac{5}{7}+\left(-\frac{2}{5}\right)$

$x=\frac{5}{7}-\frac{2}{5}$

$x=\frac{25}{35}-\frac{14}{35}$

$x=\frac{11}{35}$

Vậy $x=\frac{11}{35}$.

c) $\frac{5}{4}-6x=\frac{7}{12}$

$-6x=\frac{7}{12}-\frac{5}{4}$

$-6x=\frac{7}{12}-\frac{15}{12}$

$-6x=\frac{-8}{12}$

$x=\frac{-8}{12}:\left(-6\right)$

$x=\frac{-8}{12}\cdot \frac{-1}{6}$

$x=\frac{1}{9}$

Vậy $x=\frac{1}{9}$.

d) $3-2x-\left(\frac{5}{4}-\frac{7}{5}\right)=\frac{9}{20}$

$3-2x-\left(\frac{-3}{20}\right)=\frac{9}{20}$

$-2x=\frac{9}{20}+\left(\frac{-3}{20}\right)-3$

$-2x=\frac{6}{20}-3$

$-2x=\frac{3}{10}-\frac{30}{10}$

$-2x=\frac{-27}{10}$

$x=\frac{-27}{10}:\left(-2\right)$

$x=\frac{27}{20}$

Vậy $x=\frac{27}{20}$.

Bài 12. Tính giá trị của biểu thức sau:

a) $\left(\frac{2}{3}+\frac{1}{6}\right):\frac{5}{4}+\left(\frac{1}{4}+\frac{3}{8}\right):\frac{5}{2}$;

b) $2:{\left(\frac{1}{2}-\frac{2}{3}\right)}^2+0,{25}^3\cdot 4^3-{\left(-12\right)}^4:6^4$;

c) $7\cdot 2^3-5\cdot \left\{\left[10,51+4\cdot {\left(\frac{3}{4}-\frac{2}{5}\right)}^2\right]-{2022}^0\right\}$.

Hướng dẫn giải

a) $\left(\frac{2}{3}+\frac{1}{6}\right):\frac{5}{4}+\left(\frac{1}{4}+\frac{3}{8}\right):\frac{5}{2}$

$=\left(\frac{4}{6}+\frac{1}{6}\right)\cdot \frac{4}{5}+\left(\frac{2}{8}+\frac{3}{8}\right)\cdot \frac{2}{5}$

$=\frac{5}{6}\cdot \frac{4}{5}+\frac{5}{8}\cdot \frac{2}{5}$

$=\frac{2}{3}+\frac{1}{4}$

$=\frac{8}{12}+\frac{3}{12}$

$=\frac{11}{12}$

b) $2:{\left(\frac{1}{2}-\frac{2}{3}\right)}^2+0,{25}^3\cdot 4^3-{\left(-12\right)}^4:6^4$

$=2:{\left(-\frac{1}{6}\right)}^2+{\left(\frac{1}{4}\right)}^3\cdot 4^3-{\left(-2\cdot 6\right)}^4:6^4$

$=2\cdot \frac{1}{36}+\frac{1^3}{4^3}\cdot 4^3-{\left(-2\right)}^4\cdot {\left(6\right)}^4:6^4$

$=2\cdot 36+1-{\left(-2\right)}^4$

$=72+1-16=57$

c) $7\cdot 2^3-5\cdot \left\{\left[10,51+4\cdot {\left(\frac{3}{4}-\frac{2}{5}\right)}^2\right]-{2022}^0\right\}$

$=7\cdot 8-5\cdot \left\{\left[10,51+4\cdot {\left(\frac{7}{20}\right)}^2\right]-1\right\}$

$=56-5\cdot \left\{\left[10,51+4\cdot \frac{49}{400}\right]-1\right\}$

$=56-5\cdot \left\{\left[10,51+\frac{49}{100}\right]-1\right\}$

$=56-5\cdot \left\{\left[10,51+0,49\right]-1\right\}$

$=56-5\cdot \left\{11-1\right\}$

$=56-5\cdot 10=6$.

Bài 13. Tính một cách hợp lí.

a) $4,64+{\left(\frac{-1}{2}\right)}^3+0,6^2-3\cdot \frac{-3}{8}$;

b) $2022,123\cdot 2023+2022,123\cdot {\left(-2023\right)}^{2022-2021}$.

Hướng dẫn giải

a) $4,64+{\left(\frac{-1}{2}\right)}^3+0,6^2-3\cdot \frac{-3}{8}$

$=4,64+\frac{-1}{8}+0,36-\frac{-9}{8}$

$=\left(4,64+0,36\right)+\left(\frac{-1}{8}-\frac{-9}{8}\right)$

$=5+\left(\frac{-1}{8}+\frac{9}{8}\right)$

$=5+\frac{8}{8}=5+1=6$

b) 2022,123.2023 + 2022,123.(-2023)^{2022 - 2021}

= 2022,123.2023 + 2022,123.(-2023)

= 2022,123.[2023 + (-2023)]

= 2022,123.0 = 0

Học tốt Toán 7 Chương 1

Các bài học để học tốt Chương 1 Toán lớp 7 hay khác:

• Giải sgk Toán 7 Ôn tập chương 1

• Giải sbt Toán 7 Ôn tập chương 1