Bài 2 trang 80 Toán 8 Tập 1 Chân trời sáng tạo

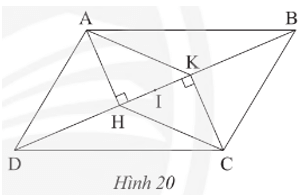
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).

Giải Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo

Bài 2 trang 80 Toán 8 Tập 1: Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).

a) Chứng minh tứ giác AHCK là hình bình hành.

b) Gọi I là trung điểm của HK. Chứng minh IB = ID.

Bài

Lời giải:

a) Do ABCD là hình bình hành nên AD // BC và AD = BC.

Do AD // BC nên $\hat{A D B} = \hat{C B D}$ (so le trong)

Xét DADH và DCBK có:

$\hat{A H D} = \hat{C K B} = 90 °$ ;

AD = BC (chứng minh trên);

$\hat{A D H} = \hat{C B K}$ (do $\hat{A D B} = \hat{C B D}$ ).

Do đó DADH = DCBK (cạnh huyền – góc nhọn).

Suy ra AH = CK (hai cạnh tương ứng).

Ta có AH ⊥ DB và CK ⊥ DB nên AH // CK.

Tứ giác AHCK có AH // CK và AH = CK nên AHCK là hình bình hành (dấu hiệu nhận biết).

b) Do AHCK là hình bình hành (câu a) nên hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của HK (giả thiết) nên I là trung điểm của AC.

Do ABCD là hình bình hành nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của AC nên I là trung điểm của BD, hay IB = ID.

Lời giải bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi hay, chi tiết khác: