Bài 4 trang 80 Toán 8 Tập 1 Chân trời sáng tạo

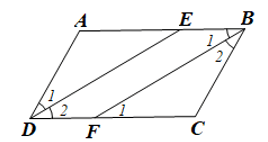
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.

Giải Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo

Bài 4 trang 80 Toán 8 Tập 1: Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F.

a) Chứng minh DE // BF.

b) Tứ giác DEBF là hình gì?

Lời giải:

Bài 4 trang 80 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

a) Do ABCD là hình bình hành nên AB // CD và .

Vì DE là tia phân giác của góc D nên ${\hat{D}}_{1} = {\hat{D}}_{2} = \frac{1}{2} \hat{D}$ .

Vì BF là tia phân giác của góc B nên ${\hat{B}}_{1} = {\hat{B}}_{2} = \frac{1}{2} \hat{B}$ .

Do đó ${\hat{B}}_{1} = {\hat{D}}_{2}$ .

Do AB // CD nên ${\hat{B}}_{1} = {\hat{F}}_{1}$ (so le trong).

Suy ra ${\hat{D}}_{2} = {\hat{F}}_{1}$

Mà hai góc này ở vị trí so le trong nên DE // BF.

b) Tứ giác DEBF có EB // FD (do AB // CD) và DE // BF nên là hình bình hành (dấu hiệu nhận biết).

Lời giải bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi hay, chi tiết khác: