Bài 8 trang 81 Toán 8 Tập 1 Chân trời sáng tạo
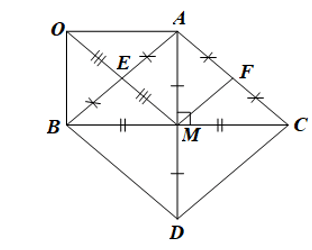
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
Giải Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo
Bài 8 trang 81 Toán 8 Tập 1: Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi.
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau.
c) Chứng minh tứ giác AEMF là hình thoi.
Lời giải:
a) Ta có D đối xứng với A qua BC nên M là trung điểm của AD và AD ⊥ BC.
Tứ giác ABDC có hai đường chéo AD và BD cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.
Lại có hai đường chéo AD ⊥ BC nên hình bình hành ABDC là hình thoi.
b) Ta có E là trung điểm của AB và OM nên hai đường chéo của tứ giác OAMB cắt nhau tại trung điểm của mỗi đường.
Do đó tứ giác OAMB là hình bình hành.
Suy ra OA // BM và OB // AM.
Ta có OB // AM và AM ⊥ BM nên OB ⊥ BM, do đó DMBO vuông tại B.
Ta có OA // BM và OB ⊥ BM nên OA ⊥ OB, do đó DAOB vuông tại O.
Do OAMB là hình bình hành nên OA = BM và OB = AM.
Xét DMBO vuông tại B và DAOB vuông tại O có:
OB = AM; BM = OA
Do đó DMBO = DAOB (hai cạnh góc vuông).
Lời giải bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi hay, chi tiết khác: