Thực hành 3 trang 78 Toán 8 Tập 1 Chân trời sáng tạo

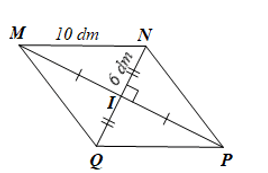
Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.

Giải Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo

Thực hành 3 trang 78 Toán 8 Tập 1: Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.

a) Tính MP khi biết MN = 10 dm, IN = 6 dm.

b) Tính $\hat{I M N}$ khi biết $\hat{M N P} = 128 °$ .

Lời giải:

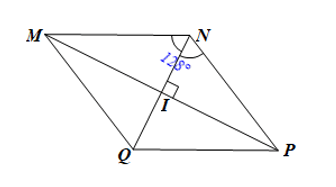
Thực hành 3 trang 78 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Do MNPQ là hình thoi nên hai đường chéo MP và NQ vuông góc với nhau tại trung điểm của mỗi đường.

Áp dụng định lí Pythagore vào DMNI vuông tại I, ta có:

MN² = MI² + NI²

Suy ra $M I = \sqrt{M N^{2} - N I^{2}} = \sqrt{10^{2} - 6^{2}} = 8$ (dm).

Do I là trung điểm của MP nên MP = 2MI = 2.8 = 16 (dm).

Vậy MP = 16 dm.

Thực hành 3 trang 78 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Vì MNPQ là hình thoi nên MQ // NP

Do đó $\hat{M N P} + \hat{N M Q} = 180 °$

Suy ra $\hat{N M Q} = 180 ° - \hat{M N P} = 180 ° - 128 ° = 52 °$ .

Do MNPQ là hình thoi nên MP và tia phân giác của góc NMQ.

Suy ra $\hat{I M N} = \frac{1}{2} \hat{N M Q} = \frac{1}{2} .52 ° = 26 °$ .

Vậy $\hat{I M N} = 26 °$ .

Lời giải bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi hay, chi tiết khác: