Bài 6 trang 81 Toán 8 Tập 1 Chân trời sáng tạo
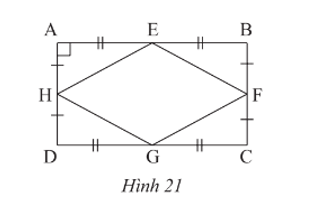
Quan sát Hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.
Giải Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo
Bài 6 trang 81 Toán 8 Tập 1: Quan sát Hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.
Lời giải:
Ta có AE = EB nên AB = 2AE.
DG = GC nên DC = 2DG.
Mà AE = DG nên AB = DC.
Chứng minh tương tự ta cũng có: AD = BC.
Tứ giác ABCD có AB = DC và AD = BC nên là hình bình hành (dấu hiệu nhận biết).
Suy ra AB // CD và AD // BC.
Lại có AD ⊥ AB nên AD ⊥ CD; AB ⊥ BC; BC ⊥ CD.
Xét DAEH và DBEF có:
; AE = BE; AH = BF.
Do đó DAEH = DBEF (hai cạnh góc vuông).
Suy ra HE = FE (hai cạnh tương ứng).
Chứng minh tương tự ta cũng có: HE = HG; HE = FG.
Do đó HE = EF = FG = GH.
Tứ giác EFGH có HE = EF = FG = GH nên là hình thoi.
Lời giải bài tập Toán 8 Bài 4: Hình bình hành – Hình thoi hay, chi tiết khác: