Luyện tập 3 trang 61 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8
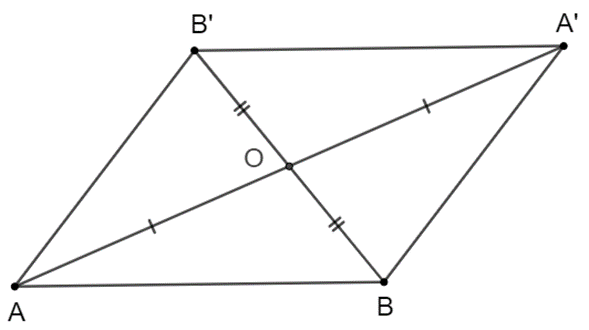
Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A’, B’ là các điểm sao cho O là trung điểm của AA’, BB’. Chứng minh rằng A’B’ = AB và đường thẳng A’B’ song song với đường thẳng AB.
Giải Toán 8 Bài 12: Hình bình hành - Kết nối tri thức
Luyện tập 3 trang 61 Toán 8 Tập 1: Cho hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB. Gọi A’, B’ là các điểm sao cho O là trung điểm của AA’, BB’. Chứng minh rằng A’B’ = AB và đường thẳng A’B’ song song với đường thẳng AB.
Lời giải:
Ta có hai điểm A, B phân biệt và điểm O không nằm trên đường thẳng AB.
Mà O là trung điểm của AA’, BB’ nên O là trung điểm của hai đường chéo của tứ giác ABA’B’.
Do đó tứ giác ABA’B’ là hình bình hành.
Suy ra A’B’ = AB (định lí 1a) và A’B’ // AB (định nghĩa hình bình hành).
Lời giải bài tập Toán 8 Bài 12: Hình bình hành hay, chi tiết khác:
HĐ2 trang 58 Toán 8 Tập 1: Hãy nêu các tính chất của hình bình hành mà em đã biết ....
HĐ3 trang 58 Toán 8 Tập 1: Cho hình bình hành ABCD (H.3.30). a) Chứng minh ∆ABC = ∆CDA ....
Câu hỏi trang 59 Toán 8 Tập 1: Hãy viết giả thiết, kết luận của Định lí 2 ....