Giải Toán 8 trang 109 Tập 2 Kết nối tri thức
Với Giải Toán 8 trang 109 Tập 2 trong Luyện tập chung trang 108, 109 Toán 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 109.
Giải Toán 8 trang 109 Tập 2 Kết nối tri thức
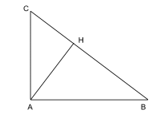
Bài 9.32 trang 109 Toán 8 Tập 2: Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.
a) Tính độ dài đoạn thẳng AH.
b) Tính độ dài các đoạn thẳng AB và AC.
Lời giải:
a) Có BC = BH + CH = 16 + 9 = 25 (cm).
Xét tam giác ABC vuông tại A có: AB2 + AC2 = BC2 (định lý Pythagore).
Xét tam giác AHC vuông tại H có: AC2 = AH2 + CH2 (định lý Pythagore).
Suy ra AH2 = AC2 – CH2 (1).
Xét tam giác AHB vuông tại H có: AH2 + BH2 = AB2 (định lý Pythagore).
Suy ra AH2 = AB2 – BH2 (2).
Xét (1) + (2), có:
2AH2 = AC2 – CH2 + AB2 – BH2
2AH2 = BC2 – CH2 – BH2 (vì AB2 + AC2 = BC2)
2AH2 = 252 – 92 – 162
2AH2 = 288
AH2 = 144
Suy ra AH = 12 (cm).
b) Có AC2 = AH2 + CH2 = 122 + 92 = 225.
Suy ra AC = 15 (cm).
Có AB2 = AH2 + BH2 = 122 + 162 = 400.
Suy ra AB = 20 (cm).
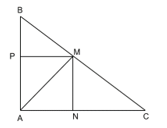
Bài 9.33 trang 109 Toán 8 Tập 2: Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.
a) Chứng minh rằng ΔBMP ∽ ΔMCN.
b) Tính độ dài đoạn thẳng AM.
Lời giải:
a) Vì BM = 4 cm; BC = 10 cm nên MC = 6 cm.
Ta thấy 62 + 82 = 102 = 100 hay AB2 + AC2 = BC2 nên tam giác ABC vuông tại A.
Lại có MN // AB (cùng vuông góc với AC) và MP // AC (cùng vuông góc với AB).
Tam giác BMP vuông tại P và tam giác MCN vuông tại N có (MP // AC và hai góc ở vị trí đồng vị) nên ∆BMP ∽ ∆MCN.
b) Tam giác BMP vuông tại P và tam giác BCA vuông tại A có góc B chung nên
∆BMP ∽ ∆BCA.
Suy ra
Do đó, cm; cm.
Suy ra AP = AB – BP = 6 – cm.
Áp dụng định lí Pythagore cho tam giác vuông APM:
AM2 = AP2 + MP2 = cm.
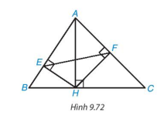
Bài 9.34 trang 109 Toán 8 Tập 2: Trong Hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:
a) ΔAEH ∽ ΔAHB;
b) ΔAFH ∽ ΔAHC;
c) ΔAFE ∽ ΔABC.
Lời giải:
a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có góc BAH chung.
Suy ra ΔAEH ∽ ΔAHB.
b) Xét hai tam giác AFH (vuông tại F) và tam giác AHC (vuông tại H) có góc CAH chung.
Suy ra ΔAFH ∽ ΔAHC.
c) Vì ΔAEH ∽ ΔAHB nên . (1)
Vì ΔAFH ∽ ΔAHC nên . (2)
Từ (1) và (2) suy ra AE . AB = AF. AC hay .
Tam giác AFE và tam giác ABC có chung; .
Do đó, ΔAFE ∽ ΔABC (c.g.c).
Bài 9.35 trang 109 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM∽ ΔHAN.
Lời giải:
Ta có:(tam giác ABC vuông tại A và tam giác HAC vuông tại H).
Xét hai tam giác HBA vuông tại H và tam giác HAC vuông tại H có (chứng minh trên) nên ∆HBA ∽ ∆HAC.
Suy ra (Vì M, N là trung điểm của AB và AC).
Xét tam giác HBM và tam giác HAN có
(chứng minh trên)
hay
Do đó ∆HBM ∽ ∆HAN (c.g.c).
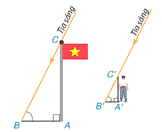
Bài 9.36 trang 109 Toán 8 Tập 2: Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.
a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?
b) Vào buổi chiều khi bóng bạn An dài 3 m, hỏi bóng cột cờ dài bao nhiêu mét?
Lời giải:
a) Ta có 60 cm = 0,6 m.
Do tam giác vuông có hai cạnh góc vuông là cột cờ và bóng của cột cờ đồng dạng với tam giác vuông có hai cạnh góc vuông là An và bóng của An (vì góc tạo bởi cạnh huyền với mỗi chiếc bóng trong mỗi tam giác là góc tạo bởi tia nắng với chiếc bóng và chúng xem như bằng nhau do mặt trời ở rất xa). Vì vậy nếu gọi h là chiều cao cột cờ ta có:
(m).
Vậy cột cờ cao 7 m.
b) Gọi k là chiều dài của bóng cột cờ vào lúc chiều, ta có:
(m).
Vậy bóng cột cờ vào buổi chiều dài 15 m.
Lời giải bài tập Toán 8 Luyện tập chung trang 108, 109 Kết nối tri thức hay khác: