Giải Toán 8 trang 123 Tập 2 Kết nối tri thức

---

Với Giải Toán 8 trang 123 Tập 2 trong Bài tập cuối chương 10 (trang 123, 124) Toán 8 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 123.

Giải Toán 8 trang 123 Tập 2 Kết nối tri thức

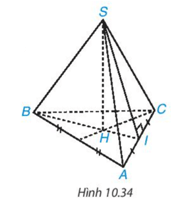
Bài 10.15 trang 123 Toán 8 Tập 2: Trung đoạn của hình chóp tam giác đều trong Hình 10.34 là:

A. SB.

B. SH.

C. SI.

D. HI.

Lời giải:

Đáp án đúng là C

Trung đoạn là SI.

Bài 10.16 trang 123 Toán 8 Tập 2: Đáy của hình chóp tứ giác đều là:

A. Hình vuông.

B. Hình bình hành.

C. Hình thoi.

D. Hình chữ nhật.

Lời giải:

Đáp án đúng là A

Đáy của hình chóp tứ giác đều là hình vuông.

Bài 10.17 trang 123 Toán 8 Tập 2: Diện tích xung quanh của hình chóp tam giác đều bằng:

A. Tích của nửa chu vi đáy và chiều cao của hình chóp.

B. Tích của nửa chu vi đáy và trung đoạn.

C. Tích của chu vi đáy và trung đoạn.

D. Tổng của chu vi đáy và trung đoạn.

Lời giải:

Đáp án đúng là B

Diện tích xung quanh của hình chóp tam giác đều bằng tích của nửa chu vi đáy và trung đoạn.

Bài 10.18 trang 123 Toán 8 Tập 2: Một hình chóp tam giác có chiều cao h, thể tích V. Diện tích đáy S là:

A. $S=\frac{h}{V}$ .

B. $S=\frac{V}{h}$.

C. $S=\frac{3V}{h}$.

D. $S=\frac{3h}{V}$ .

Lời giải:

Đáp án đúng là C

Ta có: $V=\frac{1}{3}S\cdot h\Rightarrow S=\frac{3V}{h}$.

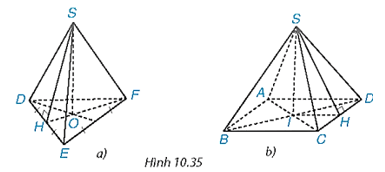
Bài 10.19 trang 123 Toán 8 Tập 2: Gọi tên đỉnh, cạnh bên, cạnh đáy, đường cao và một trung đoạn của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10.35.

Lời giải:

Hình chóp tam giác đều S.DEF

– Đỉnh: S.

– Cạnh bên: SD, SE, SF.

– Cạnh đáy: DE, DF, EF.

– Đường cao: SO.

– Một trung đoạn: SH.

Hình chóp tứ giác đều S.ABCD

– Đỉnh: S.

– Cạnh bên: SA, SB, SC, SD.

– Cạnh đáy: AB, BC, CD, AD.

– Đường cao: SI.

– Một trung đoạn: SH.

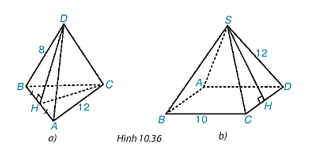
Bài 10.20 trang 123 Toán 8 Tập 2: Tính diện tích xung quanh của hình chóp tam giác đều, hình chóp tứ giác đều trong Hình 10.36.

Lời giải:

a) Nửa chu vi của tam giác ABC là: (12 + 12 + 12) : 2 = 18 (đvđd).

Ta có BH = HA = $\frac{AB}{2}=\frac{12}{2}=6$  (đvđd).

Xét tam giác HBD vuông tại H, theo định lí Pythagore suy ra: 

HD² = BD² – BH² = 8² – 6² = 28.

Suy ra HD = $\sqrt{28}$  (đvđd).

Diện tích xung quanh của hình chóp tam giác đều là 

S_xq = p . d = 18 . $\sqrt{28}$ = $18\sqrt{28}$  (đvdt).

b) Nửa chu vi hình vuông ABCD là: (10 . 4) : 2 = 20 (đvđd).

Ta có CH = HD = $\frac{CD}{2}=\frac{10}{2}=5$  (đvđd).

Xét tam giác SHD vuông tại H, theo định lí Pythagore suy ra: 

SH² = SD² – HD² = 12² – 5² = 119.

Suy ra SH = $\sqrt{119}$(đvđd).

Diện tích xung quanh của hình chóp tứ giác đều là

S_xq = p . d = 20 . $\sqrt{119}=20\sqrt{119}$  (đvdt).

Lời giải bài tập Toán 8 Bài tập cuối chương 10 (trang 123, 124) Kết nối tri thức hay khác:

• Giải Toán 8 trang 124