Bài 2 trang 69 Toán 9 Tập 2 Chân trời sáng tạo
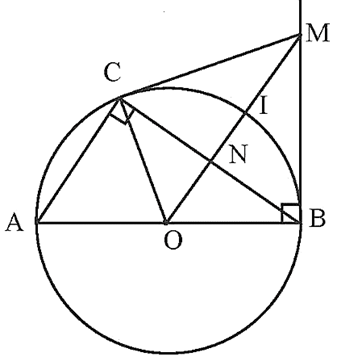
Cho tam giác ABC (AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB).
Giải Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Chân trời sáng tạo
Bài 2 trang 69 Toán 9 Tập 2: Cho tam giác ABC (AC < BC) nội tiếp đường tròn (O) có AB là đường kính. Từ điểm O vẽ đường thẳng song song với AC và cắt đường tròn (O) tại I (điểm I thuộc cung nhỏ CB).
a) Chứng minh OI vuông góc với BC.
b) Vẽ tiếp tuyến của đường tròn (O) tại B và cắt OI tại M. Chứng minh MC là tiếp tuyến của đường tròn (O).
Lời giải:
a) Ta có (góc nội tiếp chắn nửa đường tròn), suy ra AC ⊥ BC.
Mà AC // OI nên OI ⊥ BC (tính chất từ vuông góc đến song song).
b) Gọi N là giao điểm của BC và OI.
Tam giác OBC có OB = OC = R nên ∆OBC cân tại O.
Ta có ON là đường cao của ∆OBC cân tại O.
Suy ra ON cũng là đường phân giác của .
Do đó
Xét ∆COM và ∆BOM có:
OM là cạnh chung; OB = OC = R.
Do đó ∆COM = ∆BOM (c.g.c).
Suy ra (hai góc tương ứng).
Mà (BM là tiếp tuyến của đường tròn (O) tại B).
Suy ra nên OC ⊥ MC tại C.
Mà C thuộc đường tròn (O), do đó MC là tiếp tuyến của đường tròn (O).
Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay, chi tiết khác:
Khám phá 1 trang 65 Toán 9 Tập 2: Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm ....
Khám phá 2 trang 67 Toán 9 Tập 2: Gọi I là giao điểm ba đường phân giác của tam giác ABC ....