Bài 3 trang 69 Toán 9 Tập 2 Chân trời sáng tạo
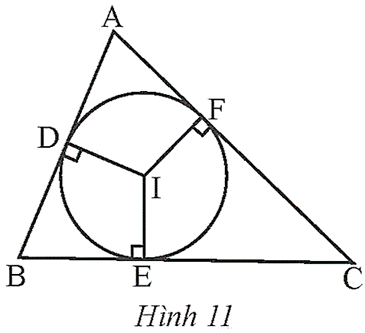
Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).
Giải Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Chân trời sáng tạo
Bài 3 trang 69 Toán 9 Tập 2: Cho tam giác ABC ngoại tiếp đường tròn (I). Gọi D, E, F lần lượt là các tiếp điểm của đường tròn (I) với các cạnh AB, BC, AC (Hình 11).
a) Chứng minh 2AD = AB + AC – BC.
b) Tìm các hệ thức tương tự như ở câu a.
Lời giải:
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có: AD = AF, BD = BE, CE = CF.
Suy ra AB + AC – BC = (AD + BD) + (AF + CF) – (BE + CE)
= (AD + AF) + (CF – CE) + (BD – BE) = 2AD.
Vậy 2AD = AB + AC – BC (đpcm).
b) Các hệ thức tương tự như ở câu a là:
2AF = AB + AC – BC;
2BD = 2BE = AB + BC – AC;
2EC = 2FC = AC + BC – AB.
Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay, chi tiết khác:
Khám phá 1 trang 65 Toán 9 Tập 2: Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm ....
Khám phá 2 trang 67 Toán 9 Tập 2: Gọi I là giao điểm ba đường phân giác của tam giác ABC ....