Khám phá 2 trang 67 Toán 9 Tập 2 Chân trời sáng tạo
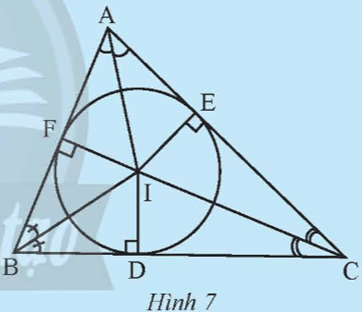
Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).
Giải Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Chân trời sáng tạo
Khám phá 2 trang 67 Toán 9 Tập 2: Gọi I là giao điểm ba đường phân giác của tam giác ABC. Vẽ ID, IE, IF lần lượt vuông góc với các cạnh BC, AC và AB (Hình 7).
a) Chứng minh rằng IE = IF = ID.
b) Vẽ đường tròn tâm I bán kính IE. Có nhận xét gì về vị trí của đường tròn này với ba cạnh của tam giác ABC?
Lời giải:
a) Xét ΔFBI vuông tại F và ΔDBI vuông tại D có:
(do BI là phân giác góc );
IB chung.
Do đó ΔFBI = ΔDBI (cạnh huyền – góc nhọn).
Suy ra IF = ID (hai cạnh tương ứng) (1).
Xét ΔIDC vuông tại D và ΔIEC vuông tại E có:
(do IC là phân giác góc );
IC chung.
Do đó ΔIDC = ΔIEC (cạnh huyền – góc nhọn).
Suy ra ID = IE (hai cạnh tương ứng) (2).
Từ (1) và (2) suy ra IE = IF = ID.
b) Đường tròn này tiếp xúc với ba cạnh của tam giác tại các điểm F, D, E.
Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay, chi tiết khác: