Thực hành 1 trang 67 Toán 9 Tập 2 Chân trời sáng tạo
Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau:
Giải Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác - Chân trời sáng tạo
Thực hành 1 trang 67 Toán 9 Tập 2: Xác định tâm và bán kính của đường tròn ngoại tiếp mỗi tam giác sau:
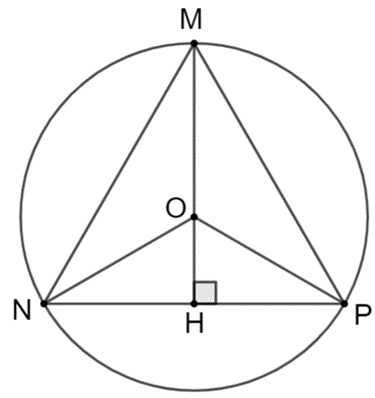
a) Tam giác đều MNP có cạnh bằng 4;
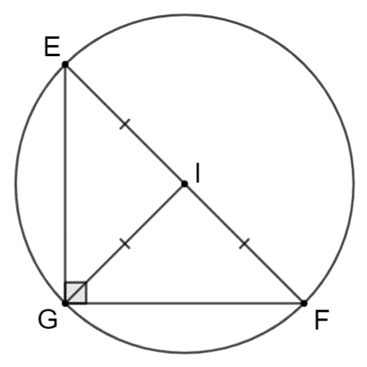
b) Tam giác EFG có EF = 5 cm; EG = 3 cm; FG = 4 cm.
Lời giải:
a) Vẽ đường cao MH của giác MNP, gọi O là điểm nằm trên MH sao cho OM = MH.
Do tam giác MNP đều nên O vừa là trọng tâm vừa là giao điểm của ba đường trung trực.
Bán kính đường tròn ngoại tiếp tam giác MNP là:
R = OH =
Do đó, đường tròn ngoại tiếp tam giác đều MNP có tâm O và bán kính
Ta có hình vẽ:
b) Xét tam giác EFG có 52 = 32 + 42 nên EF2 = EG2 + FG2.
Suy ra tam giác EFG vuông tại G.
Gọi I là trung điểm của cạnh huyền EF.
Ta có GI là đường trung tuyến ứng với cạnh huyền của tam giác EFG vuông tại G.
Suy ra IG = IE = IF = = 2,5 (cm).
Do đó, đường tròn tâm I bán kính 5 cm ngoại tiếp tam giác EFG.
Ta có hình vẽ:
Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay, chi tiết khác:
Khám phá 1 trang 65 Toán 9 Tập 2: Cho ba điểm A, B, C không thẳng hàng. Gọi O là giao điểm ....
Khám phá 2 trang 67 Toán 9 Tập 2: Gọi I là giao điểm ba đường phân giác của tam giác ABC ....