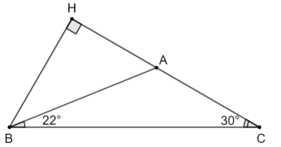
Bài 2 trang 71 Toán 9 Tập 1 Chân trời sáng tạo

Cho tam giác ABC có BC = 20 cm,

Giải Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông - Chân trời sáng tạo

Bài 2 trang 71 Toán 9 Tập 1: Cho tam giác ABC có BC = 20 cm, $\hat{A B C} = 22 °, \hat{A C B} = 30 ° .$

a) Tính khoảng cách từ điểm B đến đường thẳng AC.

b) Tính các cạnh và các góc còn lại của tam giác ABC.

c) Tính khoảng cách từ điểm A đến đường thẳng BC.

Lời giải:

a) Gọi BH là đường cao hạ từ B xuống AC.

Bài 2 trang 71 Toán 9 Tập 1 Chân trời sáng tạo

Khi đó, BH là khoảng cách từ điểm B đến đường thẳng AC.

Xét tam giác BHC có $\hat{A C H} = 30 °$ , ta có:

BH = BC . sin 30° = 20 . sin 30° = 10 (cm).

Vậy khoảng cách từ điểm B đến đường thẳng AC là 10 cm.

b) Xét tam giác ABC, ta có: $\hat{A B C} + \hat{A C B} + \hat{B A C} = 180 °$ .

Suy ra $\hat{B A C} = 180 ° - \hat{A B C} - \hat{A C B} = 180 ° - 30 ° - 22 ° = 128 ° .$

Ta có $\hat{B A H} = 180 ° - \hat{B A C} = 180 ° - 128 ° = 52 ° .$

Xét tam giác ABH vuông tại H có $\hat{B A H} = 52 °$ nên

• $A B . \sin \hat{B A H} = 10$ suy ra $A B = \frac{B H}{\sin \hat{B A H}} = \frac{10}{\sin 52 °} \approx 12, 7 (cm)$ .

• $A H . \tan \hat{B A H} = 10$ suy ra $A H = \frac{B H}{\tan \hat{B A H}} = \frac{10}{\tan 52 °} \approx 7, 8 (cm)$ .

Áp dụng định lý Pythagore vào tam giác BHC, ta có: BC² = CH² + BH²

Suy ra $C H = \sqrt{B C^{2} - B H^{2}} = \sqrt{20^{2} - 10^{2}} = 10 \sqrt{3} (cm)$ .

Do đó $A C = C H - A H \approx 10 \sqrt{3} - 7, 8 \approx 9, 5 (cm)$ .

Vậy độ dài các cạnh và các góc còn lại của tam giác ABC là $\hat{B A C} = 128 °$ , AB ≈ 7,9 cm, AC ≈ 9,5 cm.

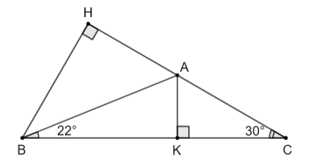
c) Gọi AK là đường cao hạ từ A xuống BC.

Khi đó, AK là khoảng cách từ điểm A đến đường thẳng BC.

Bài 2 trang 71 Toán 9 Tập 1 Chân trời sáng tạo

Xét tam giác ACK có $\hat{A C K} = 30 °$ và AC ≈ 9,5 cm nên ta có:

$A K = A C . \sin \hat{A C K} \approx 9, 5 . \sin 30 ° \approx 4, 8 (cm)$

Vậy khoảng cách từ điểm A đến đường thẳng BC khoảng 4,8 cm.

Lời giải bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông hay, chi tiết khác: