Bài 4 trang 71 Toán 9 Tập 1 Chân trời sáng tạo

---

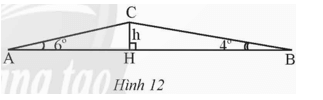
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m,

Giải Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông - Chân trời sáng tạo

Bài 4 trang 71 Toán 9 Tập 1: Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m, $\widehat{A}=6°,\widehat{B}=4°.$

a) Tính chiều cao h của con dốc.

b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.

Lời giải:

a) Đặt AH = x (m) (0 < x < 762).

Suy ra BH = 762 – x (m).

Áp dụng hệ thức về cạnh và góc trong tam giác vuông, ta có:

 h = x . tan 6° và h = (762 – x) . tan 4°.

Suy ra x . tan 6° = (762 – x) . tan 4°

x . tan 6° = 762 . tan 4° – x . tan 4°

x . tan 6° + x . tan 4° = 762 . tan 4°

x . (tan 6° + tan 4°) = 762 . tan 4°

$x=\frac{762.\tan 4°}{\tan 6°+\tan 4°}$.

Do đó $h=\frac{762.\tan 4°}{\tan 6°+\tan 4°}\cdot \tan 6°\approx 32\left(m\right)$ .

Vậy chiều cao h của con dốc khoảng 32 m.

b) Xét tam giác AHC vuông tại H có $\widehat{A}=6°$  nên h = AC . sin A.

Suy ra $AC=\frac{h}{\sin A}=\frac{32}{\sin 6°}\approx 306,1\text{\hspace{0.17em}\hspace{0.17em}(m)}=0,3061\text{\hspace{0.17em}\hspace{0.17em}(km)}$ .

Xét tam giác BHC vuông tại H có $\widehat{B}=4°$  nên h = BC . sin B.

Suy ra $BC=\frac{h}{\sin B}=\frac{32}{\sin 4°}\approx 458,7\text{\hspace{0.17em}\hspace{0.17em}(m)}=0,4587\text{\hspace{0.17em}\hspace{0.17em}(km)}$ .

Thời gian An đi từ nhà đến trường là:

$\frac{0,3061}{4}+\frac{0,4587}{19}\approx 0,1$ (giờ) = 6 phút.

Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà và đến trường vào lúc:

6 giờ + 6 phút = 6 giờ 6 phút.

Vậy bạn An đến trường lúc 6 giờ 6 phút.

Lời giải bài tập Toán 9 Bài 2: Hệ thức giữa cạnh và góc của tam giác vuông hay, chi tiết khác:

• Khởi động trang 67 Toán 9 Tập 1: Làm thế nào để tính chiều cao BC khi biết khoảng cách AB và góc A trong hình bên?....

• Khám phá 1 trang 67 Toán 9 Tập 1: Cho tam giác ABC vuông tại A (Hình 1).a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao lại có các đẳng thức: ...

• Thực hành 1 trang 68 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20 cm. Tính độ dài các cạnh góc vuông ....

• Thực hành 2 trang 68 Toán 9 Tập 1: Tính độ dài cạnh góc vuông x của mỗi tam giác vuông trong Hình 3 (kết quả làm tròn đến hàng phần trăm).....

• Vận dụng 1 trang 68 Toán 9 Tập 1: Một cần cẩu đang nâng một khối gõ trên sông. Biết tay cẩu AB có chiều dài là 16 m và nghiêng một góc 42° so với phương nằm ngang (Hình 4). ....

• Khám phá 2 trang 69 Toán 9 Tập 1: Cho tam giác ABC (Hình 5). Em hãy cho biết trong các trường hợp nào sau đây, ta có thể tính được tất cả các cạnh và các góc của tam giác. Giải thích cách tính. ....

• Vận dụng 2 trang 70 Toán 9 Tập 1: Trong Hình 9, cho OH = 4 m, $\widehat{AOH}=42°,\widehat{HOB}=28°.$ Tính chiều cao AB của dây.....

• Bài 1 trang 71 Toán 9 Tập 1: Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và $\widehat{BAC}=68°$ (Hình 10).....

• Bài 2 trang 71 Toán 9 Tập 1: Cho tam giác ABC có BC = 20 cm, $\widehat{ABC}=22°,\widehat{ACB}=30°.$ ....

• Bài 3 trang 71 Toán 9 Tập 1: Một người đẩy một vật lên hết một con dốc nghiêng một góc 35° (Hình 11). ....