c) Tính khoảng cách từ điểm A đến đường thẳng BC.
Câu hỏi:
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
Trả lời:
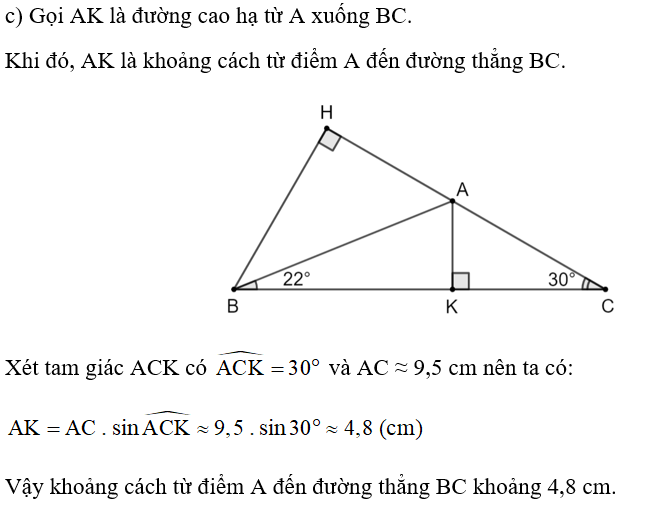
Câu hỏi:
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
Trả lời:

Câu 1:
Làm thế nào để tính chiều cao BC khi biết khoảng cách AB và góc A trong hình bên?
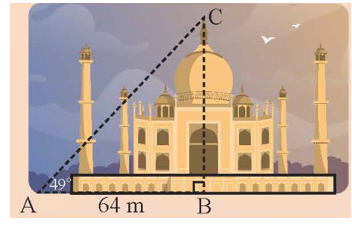
Câu 2:
Cho tam giác ABC vuông tại A (Hình 1).
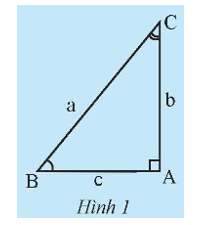
a) Hãy tính sin B theo b và a, cos B theo c và a. Sử dụng các kết quả tính được để giải thích tại sao lại có các đẳng thức: b = a . sin B; c = a . cos B.
Câu 3:
b) Hãy tính tan B theo b và c, cot B theo c và b. Sử dụng các kết quả tính được ở trên để giải thích tại sao lại có các đẳng thức: b = c . tan B; c = b . cot B.
Câu 4:
Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20 cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm):
a)
Câu 5:
Một người đẩy một vật lên hết một con dốc nghiêng một góc 35° (Hình 11).
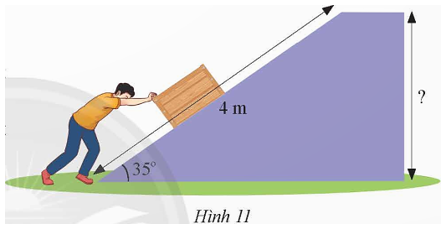
Tính độ cao của vật so sới mặt đất biết độ dài con dốc là 4 m.
Câu 6:
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B). Khi đi từ A đến B, An phải đi đoạn lên dốc AC và đoạn xuống dốc CB (Hình 12). Biết AB = 762 m,
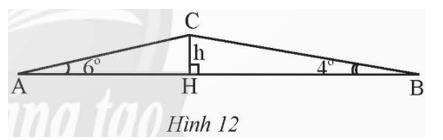
a) Tính chiều cao h của con dốc.
Câu 7:
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ khi lên dốc là 4 km/h và tốc độ khi xuống dốc là 19 km/h.
