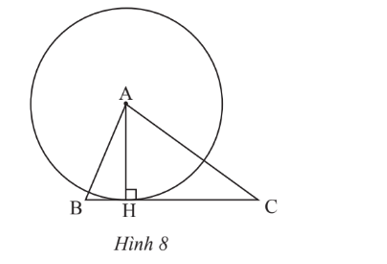
Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.
Câu hỏi:
Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.
Trả lời:
Ta có BC đi qua H thuộc đường tròn (A; AH) và BC ⊥ AH nên BC là tiếp tuyến của đường tròn (A; AH).
Xem thêm lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết:
Câu 1:
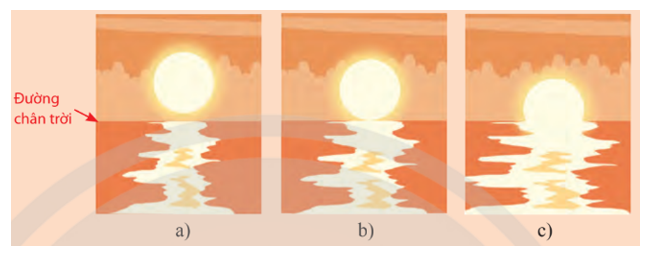
Hãy mô tả các vị trí của Mặt Trời so với đường chân trời ở các thời điểm Mặt Trời lặn khác nhau trong hình dưới đây.
Xem lời giải »
Câu 2:
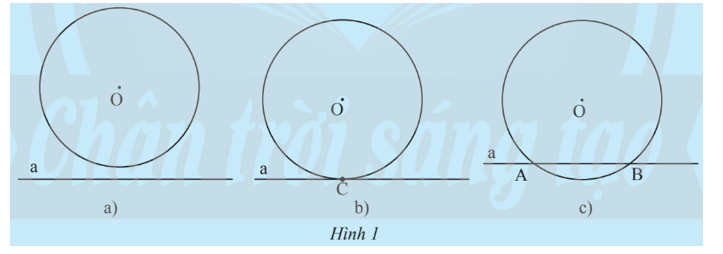
Nêu nhận xét về số điểm chung của đường thẳng a và đường tròn (O) trong mỗi hình sau:
Xem lời giải »
Câu 3:
Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:
a) d = 4 cm;
b) d = 5 cm;
c) d = 6 cm.
Xem lời giải »
Câu 4:
Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.
Xem lời giải »
Câu 5:
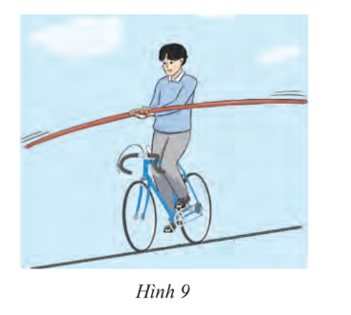
Một diễn viên xiếc đi xe đạp trên một sợi dây cáp căng (Hình 9). Ta coi sợi dây là tiếp tuyến của mỗi bánh xe, xác định các tiếp điểm.
Xem lời giải »
Câu 6:
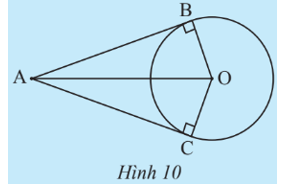
Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).
a) Chứng minh hai tam giác ABO và ACO bằng nhau.
b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.
Xem lời giải »
Câu 7:
Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết
a) Tính số đo và
Xem lời giải »