Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường
Câu hỏi:
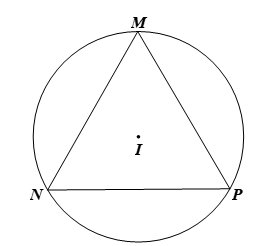
Cho tam giác đều MNP có ba đỉnh nằm trên đường tròn (I). Hãy chỉ ra các góc nội tiếp của đường tròn (I) và tính số đo của các góc nội tiếp đó.
Trả lời:
Xét đường tròn (I), ta có các góc nội tiếp đường tròn là:
Vì ∆MNP là tam giác đều nên
Xem thêm lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết:
Câu 1:
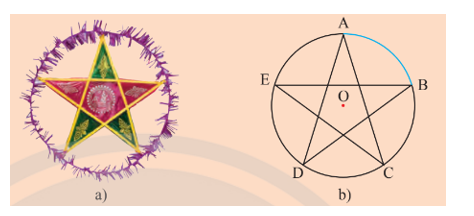
Hình ngôi sao năm cánh trong Hình a được vẽ lại như Hình b. Phần tô màu xanh trên đường tròn từ điểm A đến điểm B được gọi là gì? Làm thế nào để biểu diễn số đo của nó?
Xem lời giải »
Câu 2:
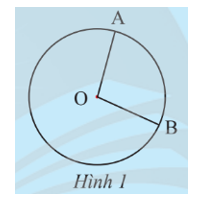
Cho hai điểm A, B trên đường tròn (O; R). Nêu nhận xét về đỉnh và cạnh của
Xem lời giải »
Câu 3:
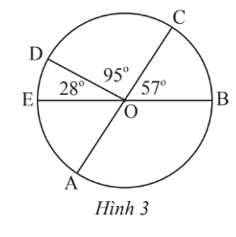
Tính số đo góc ở tâm và trong Hình 3. Biết AC và BE là hai đường kính của đường tròn (O).
Xem lời giải »
Câu 4:
Tính số đo góc ở tâm được tạo thành khi kim giờ quay:
a) Từ 7 giờ đến 9 giờ;
b) Từ 9 giờ đến 12 giờ.
Xem lời giải »
Câu 5:
Cho hai điểm E và F nằm trên đường tròn (O). Có bao nhiêu góc nội tiếp chắn cung EF?
Xem lời giải »
Câu 6:
Cho đường tròn (O; 5 cm) và điểm M sao cho OM = 10 cm. Qua M vẽ hai tiếp tuyến với đường tròn tại A và B. Tính số đo góc ở tâm được tạo bởi hai tia OA và OB.
Xem lời giải »
Câu 7:
Cho tam giác đều ABC. Vẽ nửa đường tròn đường kính BC cắt cạnh AB và AC lần lượt tại D và E. Hãy so sánh các cung
Xem lời giải »