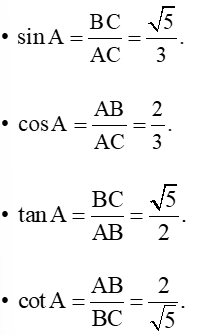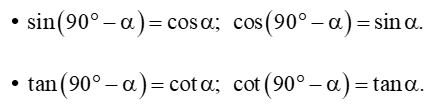Lý thuyết Toán 9 Tỉ số lượng giác của góc nhọn - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Tỉ số lượng giác của góc nhọn - Chân trời sáng tạo

Lý thuyết Tỉ số lượng giác của góc nhọn

1. Định nghĩa tỉ số lượng giác của góc nhọn

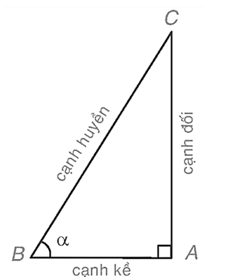
Cho tam giác ABC vuông tại A có góc nhọn B bằng α. Ta gọi AC là cạnh đối của góc α, AB là cạnh kề của góc α.

Xét tam giác ABC vuông tại A có $\widehat{ABC}=\alpha ,$ ta có:

• Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu sin α.

• Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu cos α.

• Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu tan α.

• Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu cot α.

Chú ý: Với góc nhọn α, ta có:

• 0 < sin α < 1; 0 < cos α < 1.

• $\cot \alpha =\frac{1}{\tan \alpha }.$

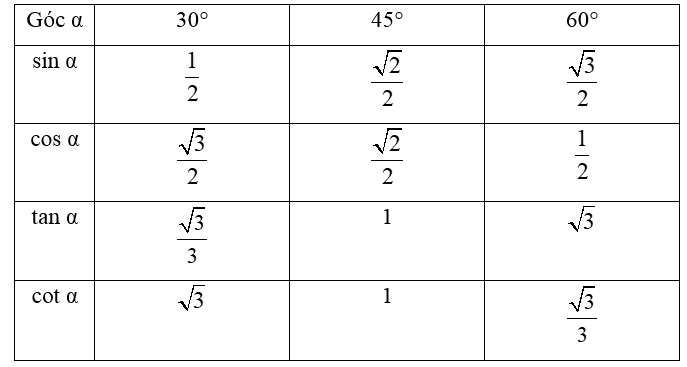
• Ta có bảng tỉ số lượng giác của các góc 30°, 45°, 60° như sau:

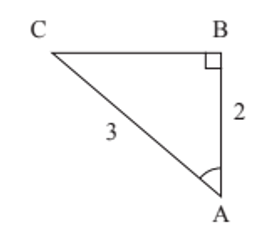
Ví dụ 1: Cho tam giác ABC vuông tại B có AB = 2, AC = 3. Tính các tỉ số lượng giác của góc nhọn A.

Hướng dẫn giải

Theo định lí Pythagore, ta có: AC² = AB² + BC²

Nên BC² = AC² – AB² = 3² − 2² = 5 nên $BC=\sqrt{5}.$

Ta có các tỉ số lượng giác của góc A là:

Vậy $\sin A=\frac{\sqrt{5}}{3},\cos A=\frac{2}{3},\tan A=\frac{\sqrt{5}}{2},\cot A=\frac{2}{\sqrt{5}}.$

Ví dụ 2: Tính giá trị của biểu thức $A=\frac{\sin 60°.\cos 30°}{\cot 45°}.$

Hướng dẫn giải

Ta có: $A=\frac{\sin 60°.\cos 30°}{\cot 45°}=\frac{\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}}{1}=\frac{3}{4}.$

2. Tỉ số lượng giác của hai góc phụ nhau

• Hai góc được gọi là phụ nhau nếu chúng có tổng bằng 90°. Như vậy, góc phụ của góc nhọn α là góc (90° − α).

• Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Chú ý: Khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta có thể viết sin A thay cho $\sin \widehat{A}.$

Ví dụ: So sánh:

a) sin 65° và cos 35°;

b) tan 15° và cot 70°.

Hướng dẫn giải

a) Ta có: $\sin 65°=\cos \left(90°-65°\right)=\cos 25°$ mà 25° < 35°.

Suy ra, sin 65° < cos 35°.

b) Ta có: $\tan 15°=\cot \left(90°-15°\right)=\cot 75°$ mà 75° > 70°.

Suy ra, tan 15° > cot 70°.

Bài tập Tỉ số lượng giác của góc nhọn

Bài 1. Cho α là góc nhọn bất kỳ. Chọn khẳng định đúng.

A. $\sin \alpha +\cos \alpha =1;$

B. ${\sin }^2\alpha +{\cos }^2\alpha =1;$

C. ${\sin }^3\alpha +{\cos }^3\alpha =1;$

D. $\sin \alpha -\cos \alpha =1.$

Hướng dẫn giải

Đáp án đúng là: B

Cho α là góc nhọn bất kỳ, khi đó ${\sin }^2\alpha +{\cos }^2\alpha =1.$

Bài 2. Cho α là góc nhọn bất kỳ. Chọn khẳng định sai.

A. $\tan \alpha =\frac{\sin \alpha }{\cos \alpha };$

B. $\cot \alpha =\frac{\cos \alpha }{\sin \alpha };$

C. $\tan \alpha .\cot \alpha =1;$

D. ${\tan }^2\alpha -1={\cos }^2\alpha .$

Hướng dẫn giải

Đáp án đúng là: D

Cho α là góc nhọn bất kỳ, khi đó:

• ${\sin }^2\alpha +{\cos }^2\alpha =1;$$\tan \alpha .\cot \alpha =1.$

• $\tan \alpha =\frac{\sin \alpha }{\cos \alpha };$$\cot \alpha =\frac{\cos \alpha }{\sin \alpha }.$

• $1+{\tan }^2\alpha =\frac{1}{{\cos }^2\alpha };$$1+{\cot }^2\alpha =\frac{1}{{\sin }^2\alpha }.$

Bài 3. Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác của góc B trong mỗi trường hợp sau:

a) BC = 12 cm; AB = 8 cm;

b) $AB=a\sqrt{2};$$AC=2\sqrt{2}a.$

Hướng dẫn giải

a) Theo định lí Pythagore, ta có: BC² = AB² + AC²

Suy ra AC² = BC² – AB² = 12² – 8² = 80.

Do đó $AC=4\sqrt{5}$ cm.

Các tỉ số lượng giác của góc B là:

• $\sin B=\frac{AC}{BC}=\frac{4\sqrt{5}}{12}=\frac{\sqrt{5}}{3};$$\cos B=\frac{AB}{BC}=\frac{8}{12}=\frac{2}{3}.$

• $\tan B=\frac{AC}{AB}=\frac{4\sqrt{5}}{8}=\frac{\sqrt{5}}{2};$$\cot B=\frac{AB}{AC}=\frac{2}{\sqrt{5}}=\frac{2\sqrt{5}}{5}.$

Vậy $\sin B=\frac{\sqrt{5}}{3};\cos B=\frac{2}{3};\tan B=\frac{\sqrt{5}}{2};\cot B=\frac{2\sqrt{5}}{5}.$

b) Theo định lí Pythagore, ta có: BC² = AB² + AC²

$={\left(a\sqrt{2}\right)}^2+{\left(2\sqrt{2}a\right)}^2$$=2a^2+8a^2$$=10a^2$

Suy ra $BC=a\sqrt{10}.$

Các tỉ số lượng giác của góc B là:

• $\sin B=\frac{AC}{BC}=\frac{2\sqrt{2}a}{a\sqrt{10}}=\frac{2\sqrt{5}a}{5};$$\cos B=\frac{AB}{BC}=\frac{a\sqrt{2}}{a\sqrt{10}}=\frac{\sqrt{5}}{5}.$

• $\tan B=\frac{AC}{AB}=\frac{2\sqrt{2}a}{a\sqrt{2}}=2;$$\cot B=\frac{1}{\tan B}=\frac{1}{2}.$

Vậy $\sin B=\frac{2\sqrt{5}a}{5};\cos B=\frac{\sqrt{5}}{5};\tan B=2;\cot B=\frac{1}{2}.$

Bài 4. Rút gọn và tính các biểu thức sau:

a) $A=\sin 15°-\sin 60°+\cos 30°-\cos 75°+5;$

b) $B={\sin }^{2}82°+\cot 24°.\cot 66°+{\cos }^{2}82°.$

Hướng dẫn giải

a) Ta có: $A=\sin 15°-\sin 60°+\cos 30°-\cos 75°+5$

$=\left(\sin 15°-\cos 75°\right)+\left(\cos 30°-\sin 60°\right)+5$

$=\left(\cos 75°-\cos 75°\right)+\left(\cos 30°-\cos 30°\right)+5$

= 0 + 0 + 5 = 5.

b) Ta có: $B={\sin }^{2}82°+\cot 24°.\cot 66°+{\cos }^{2}82°$

$=\left({\sin }^{2}82°+{\cos }^{2}82°\right)+\cot 24°.\cot 66°$

$=1+\tan 66°.\cot 66°$

= 1 + 1 = 2.

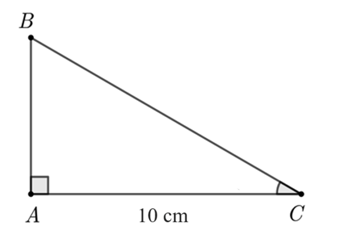
Bài 5. Cho tam giác ABC vuông tại A có AC = 10 cm, $\cos A=\frac{1}{2}.$ Tính  sinA và độ dài cạnh AB và BC.

Hướng dẫn giải

Ta có: ${\sin }^{2}A+{\cos }^{2}A=1$ suy ra ${\sin }^{2}A=1-{\cos }^{2}A.$ 

Do đó $\sin A=\sqrt{1-{\cos }^{2}A}.$

• Thay $\cos A=\frac{1}{2},$ ta có: $\sin A=\sqrt{1-{\left(\frac{1}{2}\right)}^2}=\frac{\sqrt{3}}{2}$ (do sin A > 0 vì góc A nhọn).

Ta lại có: $\cos A=\frac{AB}{AC}$ suy ra AB = AC.cos A.

• Thay $\cos A=\frac{1}{2},$ AC = 10 cm, ta có: $AB=10\cdot \frac{1}{2}=5$ (cm).

Mà $\sin A=\frac{BC}{AC}$ suy ra BC = AC.sin A.

• Thay $\sin A=\frac{\sqrt{3}}{2},$ AC = 10 cm, ta có: $BC=10\cdot \frac{\sqrt{3}}{2}=5\sqrt{3}$ (cm)

Vậy $\sin A=\frac{\sqrt{3}}{2},$AB = 5 cm, $BC=5\sqrt{3}$ cm

Học tốt Tỉ số lượng giác của góc nhọn

Các bài học để học tốt Tỉ số lượng giác của góc nhọn Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn