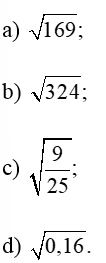Lý thuyết Toán 9 Căn bậc hai - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 1: Căn bậc hai sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Căn bậc hai - Chân trời sáng tạo

Lý thuyết Căn bậc hai

1. Căn bậc hai

• Cho số thực a không âm. Số thực x thỏa mãn x² = a được gọi là một căn bậc hai của a.

• Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là $\sqrt{a}$ (căn bậc hai số học của a), số âm là $-\sqrt{a}$

• Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết $\sqrt{0}=0.$

Chú ý:

• Số âm không có căn bậc hai.

• Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).

• Ở lớp 7 ta đã biết, nếu a > b > 0 thì $\sqrt{a}>\sqrt{b}.$ Từ đó suy ra

$-\sqrt{a}<-\sqrt{b}<0<\sqrt{b}<\sqrt{a}.$

Ví dụ: Tìm các căn bậc hai của mỗi số sau:

a) 36;

b) $\frac{4}{9}$

c) 0,04.

Hướng dẫn giải

a) Ta có 6² = 36, nên 36 có hai căn bậc hai là 6 và −6.

b) Ta có ${\left(\frac{2}{3}\right)}^2=\frac{4}{9},$ nên $\frac{4}{9}$ có hai căn bậc hai là $\frac{2}{3}$ và $-\frac{2}{3}$

c) Ta có (0,2)² = 0,04, nên 0,04 có hai căn bậc hai là 0,2 và −0,2.

2. Căn thức bậc hai

• Với A là một biểu thức đại số, ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn.

Chú ý:

• Ta cũng nói $\sqrt{A}$ là một biểu thức. Biểu thức $\sqrt{A}$ xác định (hay có nghĩa) khi A nhận giá trị không âm.

• Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức $\sqrt{A}$

Ví dụ: Cho biểu thức $P=\sqrt{13-2x}.$

a) Với giá trị nào của x thì biểu thức P xác định?

b) Tính giá trị của biểu thức A khi x = 2.

Hướng dẫn giải

a) Biểu thức P xác định khi 13 – 2x ≥ 0 hay 2x ≤ 13 hay $x\le \frac{13}{2}.$

b) Ta thấy x = 2 thỏa mãn điều kiện xác định và khi x = 2 ta có $P=\sqrt{13-2.2}=\sqrt{9}=3.$

Bài tập Căn bậc hai

Bài 1. Tính:

Hướng dẫn giải

a) Ta có 10² = 100 nên $\sqrt{100}=10.$

b) Ta có 18² = 324 nên $\sqrt{324}=18.$

c) Ta có ${\left(\frac{3}{5}\right)}^2=\frac{9}{25}$ nên $\sqrt{\frac{9}{25}}=\frac{3}{5}.$

d) Ta có (0,4)² = 0,16 nên $\sqrt{0,16}=0,4.$

Bài 2. Tìm x, biết:

a) x² = 144;

b) 2x² = 8;

c) 3x² = 10.

Hướng dẫn giải

a) Ta có 12² = 144 nên x = 12 hoặc x = −12.

b) Ta có 2x² = 8 suy ra x² = 4. Mà 2² = 4 nên x = 2 hoặc x = −2.

c) Ta có 3x² = 10 suy ra $x^2=\frac{10}{3}.$ Mà ${\left(\sqrt{\frac{10}{3}}\right)}^2=\frac{10}{3}$ nên $x=\frac{10}{3}$ hoặc $x=-\frac{10}{3}.$

Bài 3. Cho biểu thức $A=\sqrt{x^2-2xy+2}.$ Tính giá trị của A khi:

a) x = 2, y = −3.

b) x = 1, y = 5.

c) x = −4, y = 4.

Hướng dẫn giải

a) Khi x = 2 và y = −3, ta có $A=\sqrt{2^2-\mathrm{2.2.}\left(-3\right)+2}=\sqrt{18}=3\sqrt{2}.$

b) Khi x = 1 và y = 5, ta có $A=\sqrt{1^2-\mathrm{2.1.5}+2}=\sqrt{-7}$ (không xác định vì −7 < 0).

c) Khi x = −4 và y = 4, ta có $A=\sqrt{4^2-\mathrm{2.4.4}+2}=\sqrt{-14}$ (không xác định vì −14 < 0).

Học tốt Căn bậc hai

Các bài học để học tốt Căn bậc hai Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 1: Căn bậc hai