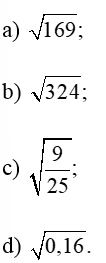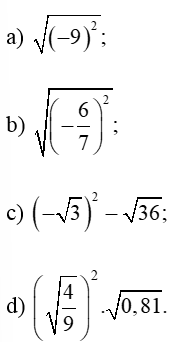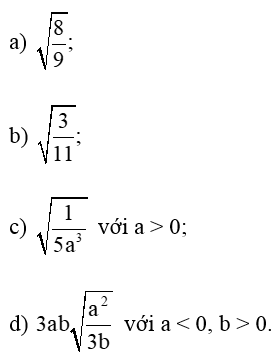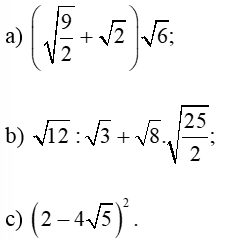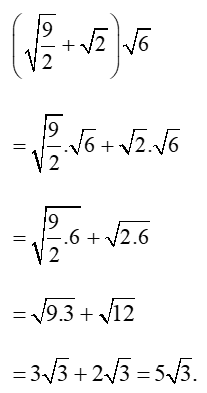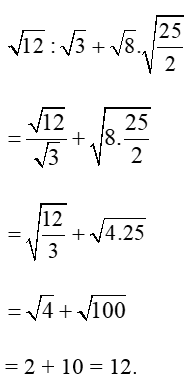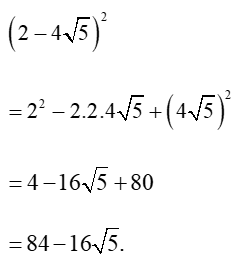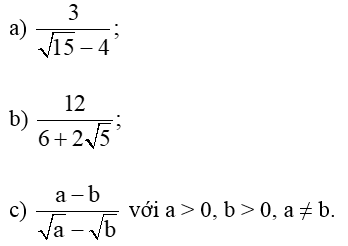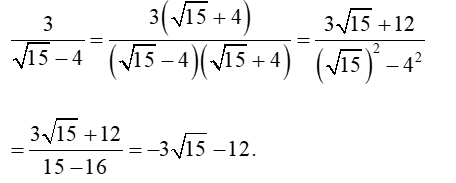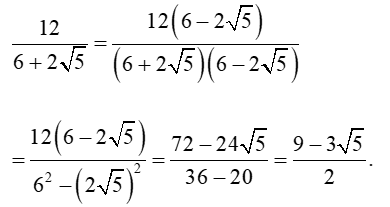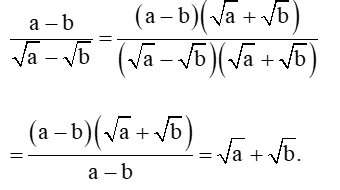Tổng hợp lý thuyết Toán 9 Chương 3 - Chân trời sáng tạo

---

Tổng hợp lý thuyết Toán 9 Chương 3: Căn thức sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 3.

Tổng hợp lý thuyết Toán 9 Chương 3 - Chân trời sáng tạo

Tóm tắt lý thuyết Chương 3

1. Căn bậc hai

• Cho số thực a không âm. Số thực x thỏa mãn x² = a được gọi là một căn bậc hai của a.

• Mỗi số dương a có đúng hai căn bậc hai là hai số đối nhau: số dương là $\sqrt{a}$ (căn bậc hai số học của a), số âm là $-\sqrt{a}$

• Số 0 chỉ có đúng một căn bậc hai là chính nó, ta viết $\sqrt{0}=0.$

Chú ý:

• Số âm không có căn bậc hai.

• Phép toán tìm căn bậc hai số học của số không âm gọi là phép khai căn bậc hai hay phép khai phương (gọi tắt là khai phương).

• Ở lớp 7 ta đã biết, nếu a > b > 0 thì $\sqrt{a}>\sqrt{b}.$ Từ đó suy ra

$-\sqrt{a}<-\sqrt{b}<0<\sqrt{b}<\sqrt{a}.$

2. Căn thức bậc hai

• Với A là một biểu thức đại số, ta gọi $\sqrt{A}$ là căn thức bậc hai của A, còn A được gọi là biểu thức lấy căn hoặc biểu thức dưới dấu căn.

Chú ý:

• Ta cũng nói $\sqrt{A}$ là một biểu thức. Biểu thức $\sqrt{A}$ xác định (hay có nghĩa) khi A nhận giá trị không âm.

• Khi A nhận giá trị không âm nào đó, khai phương giá trị này ta nhận được giá trị tương ứng của biểu thức $\sqrt{A}$

3. Căn bậc ba của một số

• Cho số thực a. Số thực x thỏa mãn x³ = a được gọi là căn bậc ba của a.

• Mỗi số thực a đều có đúng một căn bậc ba, kí hiệu là $\sqrt[3]{a}.$

• Trong kí hiệu $\sqrt[3]{a},$ số 3 được gọi là chỉ số căn. Phép toán tìm căn bậc ba của một số gọi là phép khai căn bậc ba.

Chú ý:

• Từ định nghĩa căn bậc ba, ta có ${\left(\sqrt[3]{a}\right)}^3=\sqrt[3]{a^3}=a.$

4. Căn thức bậc ba

• Với A là một biểu thức đại số, ta gọi $\sqrt[3]{A}$ là căn thức bậc ba của A.

5. Căn thức bậc hai của một bình phương

• Với mọi số thực a, ta có $\sqrt{a^2}=\left|a\right|.$

• Với biểu thức A bất kì, ta có $\sqrt{A^2}=\left|A\right|,$ nghĩa là

+ $\sqrt{A^2}=A$ khi A ≥ 0 (tức là khi A nhận giá trị không âm)

+ $\sqrt{A^2}=-A$ khi A < 0 (tức là khi A nhận giá trị âm)

6. Căn thức bậc hai của một tích

• Với hai số thực a và b không âm, ta có:

$\sqrt{a.b}=\sqrt{a}.\sqrt{b}.$

• Với hai biểu thức A và B nhận giá trị không âm, ta có:

$\sqrt{A.B}=\sqrt{A}.\sqrt{B}.$

• Với số thực a bất kì và b không âm, ta có

$\sqrt{a^{2}b}=\left|a\right|\sqrt{b}.$

+ Biến đổi này được gọi là đưa thừa số ra ngoài dấu căn.

• Ngược lại, ta có biến đổi đưa thừa số vào trong dấu căn:

+ Nếu a ≥ 0 thì $a\sqrt{b}=\sqrt{a^{2}b}.$

+ Nếu a < 0 thì $a\sqrt{b}=-\sqrt{a^{2}b}.$

Nhận xét: Tổng quát hơn, với hai biểu thức A, B mà B ≥ 0, ta có $\sqrt{A^{2}B}=\left|A\right|\sqrt{B}.$

7. Căn thức bậc hai của một thương

• Với số thực a không âm và số thực b dương, ta có

$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}.$

• Với biểu thức A nhận giá trị không âm và biểu thức B nhận giá trị dương, ta có

$\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}.$

8. Trục căn thức ở mẫu

• Đối với những biểu thức chứa căn thức ở mẫu, ta thường biến đổi để khử căn thức ở mẫu đó. Phép biến đổi như vậy gọi là trục căn thức ở mẫu.

• Với biểu thức $\frac{\sqrt{a}}{\sqrt{b}}$ (a ≥ 0, b > 0), ta biến đổi:

$\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{a}.\sqrt{b}}{\sqrt{b}.\sqrt{b}}=\frac{\sqrt{ab}}{b}.$

Chú ý:

• Với số thực a không âm và số thực b dương, ta thường biến đổi

$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{a}.\sqrt{b}}{\sqrt{b}.\sqrt{b}}=\frac{\sqrt{ab}}{b}$ hoặc $\sqrt{\frac{a}{b}}=\sqrt{\frac{ab}{b^2}}=\frac{\sqrt{ab}}{\sqrt{b^2}}=\frac{\sqrt{ab}}{b}$

để khử mẫu của biểu thức dưới dấu căn.

• Tổng quát hơn, với hai biểu thức A và B thỏa mãn AB ≥ 0, B ≠ 0, ta có:

$\sqrt{\frac{A}{B}}=\sqrt{\frac{AB}{B^2}}=\frac{\sqrt{AB}}{\sqrt{B^2}}=\frac{\sqrt{AB}}{\left|B\right|}.$

Chú ý:

• Trong câu a của ví dụ trên, để trục căn thức ở mẫu, ta nhân cả tử và mẫu với biểu thức $\sqrt{5}+1.$ Ta gọi biểu thức $\sqrt{5}-1$ và biểu thức $\sqrt{5}+1$ là hai biểu thức liên hợp với nhau.

• Với hai biểu thức A, B mà B > 0, ta có $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}.$

• Với các biểu thức A, B, C mà A ≥ 0 và A ≠ B², ta có

$\frac{C}{\sqrt{A}+B}=\frac{C\left(\sqrt{A}-B\right)}{A-B^2};$$\frac{C}{\sqrt{A}-B}=\frac{C\left(\sqrt{A}+B\right)}{A-B^2}.$

• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0 và A ≠ B, ta có

$\frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C\left(\sqrt{A}-\sqrt{B}\right)}{A-B};$$\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C\left(\sqrt{A}+\sqrt{B}\right)}{A-B}.$

9. Rút gọn biểu thức chứa căn thức bậc hai

• Để rút gọn biểu thức chứa căn thức bậc hai, ta thường vận dụng thích hợp các tính chất (giao hoán, kết hợp, phân phối) của các phép tính, quy tắc về thứ tự thực hiện phép tính và các phép biến đổi đã biết.

Bài tập ôn tập Chương 3

Bài 1. Tính:

Hướng dẫn giải

a) Ta có 10² = 100 nên $\sqrt{100}=10.$

b) Ta có 18² = 324 nên $\sqrt{324}=18.$

c) Ta có ${\left(\frac{3}{5}\right)}^2=\frac{9}{25}$ nên $\sqrt{\frac{9}{25}}=\frac{3}{5}.$

d) Ta có (0,4)² = 0,16 nên $\sqrt{0,16}=0,4.$

Bài 2. Tìm x, biết:

a) x² = 144;

b) 2x² = 8;

c) 3x² = 10.

Hướng dẫn giải

a) Ta có 12² = 144 nên x = 12 hoặc x = −12.

b) Ta có 2x² = 8 suy ra x² = 4. Mà 2² = 4 nên x = 2 hoặc x = −2.

c) Ta có 3x² = 10 suy ra $x^2=\frac{10}{3}.$ Mà ${\left(\sqrt{\frac{10}{3}}\right)}^2=\frac{10}{3}$ nên $x=\frac{10}{3}$ hoặc $x=-\frac{10}{3}.$

Bài 3. Cho biểu thức $A=\sqrt{x^2-2xy+2}.$ Tính giá trị của A khi:

a) x = 2, y = −3.

b) x = 1, y = 5.

c) x = −4, y = 4.

Hướng dẫn giải

a) Khi x = 2 và y = −3, ta có $A=\sqrt{2^2-\mathrm{2.2.}\left(-3\right)+2}=\sqrt{18}=3\sqrt{2}.$

b) Khi x = 1 và y = 5, ta có $A=\sqrt{1^2-\mathrm{2.1.5}+2}=\sqrt{-7}$ (không xác định vì −7 < 0).

c) Khi x = −4 và y = 4, ta có $A=\sqrt{4^2-\mathrm{2.4.4}+2}=\sqrt{-14}$ (không xác định vì −14 < 0).

Bài 4. Tính giá trị của các biểu thức:

a) $P=\sqrt[3]{27}+{\left(\sqrt[3]{-8}\right)}^3;$

b) $Q=\sqrt[3]{1000}-\sqrt[3]{0,008}.$

Hướng dẫn giải

a) Ta có: $P=\sqrt[3]{27}+{\left(\sqrt[3]{-8}\right)}^3$

= 3 + (−8)

= 3 – 8 = −5.

Vậy P = −5.

b) Ta có: $Q=\sqrt[3]{1000}-\sqrt[3]{0,008}$

= 10 – 0,2 = 9,8.

Vậy Q = 9,8.

Bài 5. Tìm căn bậc ba của mỗi số sau:

a) −125;

b) 216;

c) $2\frac{10}{27}.$

Hướng dẫn giải

a) Ta có (−5)³ = −125, suy ra $\sqrt[3]{-125}=-5.$

b) Ta có 6³ = 216, suy ra $\sqrt[3]{216}=6.$

c) Ta có $2\frac{10}{27}=\frac{64}{27}$ mà ${\left(\frac{4}{3}\right)}^3=\frac{64}{27}.$ Suy ra $\sqrt[3]{2\frac{10}{27}}=\frac{4}{3}.$

Bài 6. Tìm x, biết:

a) x³ = 0,027;

b) $\sqrt[3]{x}=4;$

c) $\sqrt[3]{x}=0,7.$

Hướng dẫn giải

a) Ta có 0,3³ = 0,027, suy ra x = 0,3.

b) Ta có 4³ = 64 suy ra $x={\left(\sqrt[3]{x}\right)}^3=4^3=64.$

c) Ta có (0,7)³ = 0,343 suy ra $x={\left(\sqrt[3]{x}\right)}^3=0,7^3=0,343.$

Bài 7. Tính:

Hướng dẫn giải

a) Ta có: $\sqrt{{\left(-9\right)}^2}=\left|-9\right|=9.$

b) Ta có: $\sqrt{{\left(-\frac{6}{7}\right)}^2}=\left|-\frac{6}{7}\right|=\frac{6}{7}.$

c) Ta có: ${\left(-\sqrt{3}\right)}^2-\sqrt{36}=3-6=-3.$

d) ${\left(\sqrt{\frac{4}{9}}\right)}^2.\sqrt{0,81}=\frac{4}{9}.0,9=\frac{4}{9}.\frac{9}{10}=\frac{2}{5}.$

Bài 8. Rút gọn các biểu thức sau:

a) $\sqrt{7^2.5};$

b) $\sqrt{100a^2}$ với a < 0;

c) $\sqrt{6b}.\sqrt{24b}-4b$ với b ≥ 0.

Hướng dẫn giải

a) Ta có: $\sqrt{7^2.5}=7\sqrt{5}.$

b) Ta có: $\sqrt{100a^2}=\sqrt{{\left(10a\right)}^2}=\left|10a\right|=-10a$ với a < 0.

c) Với b ≥ 0, ta có:

$\sqrt{6b}.\sqrt{24b}-4b=\sqrt{6b.24b}-4b=\sqrt{144b^2}-4b$

$=\sqrt{{\left(12b\right)}^2}-4b=\left|12b\right|-4b=12b-4b=8b$

Bài 9. Cho hình chữ nhật có chiều rộng a (cm), chiều dài b (cm) và diện tích S (cm²).

a) Tìm S, biết $a=\sqrt{6},$ $b=\sqrt{48};$

b) Tìm a, biết $S=5\sqrt{6},$ $b=\sqrt{3}.$

Hướng dẫn giải

a) Ta có: S = a.b

$=\sqrt{6}.\sqrt{48}$$=\sqrt{6.48}$

=$\sqrt{288}$$=12\sqrt{2}$

Vậy $S=12\sqrt{2}$ cm².

b) Ta có: a = S : b

$=5\sqrt{6}:\sqrt{3}$

$=5\sqrt{\frac{6}{3}}$$=5\sqrt{2}$

Vậy $a=5\sqrt{2}$cm

Bài 10. Khử mẫu của biểu thức lấy căn:

Hướng dẫn giải

a) Ta có: $\sqrt{\frac{8}{9}}=\frac{\sqrt{8}}{\sqrt{9}}=\frac{2\sqrt{2}}{3}.$

b) Ta có: $\sqrt{\frac{3}{11}}=\frac{\sqrt{3}}{\sqrt{11}}=\frac{\sqrt{3}.\sqrt{11}}{11}=\frac{\sqrt{33}}{11}.$

c) Ta có: $\sqrt{\frac{1}{5a^3}}=\frac{\sqrt{1}}{\sqrt{5a^3}}=\frac{1}{\sqrt{5a.a^2}}=\frac{1}{a\sqrt{5a}}=\frac{\sqrt{5a}}{5a^2}$ với a > 0.

d) Ta có: $3ab\sqrt{\frac{a^2}{3b}}=3ab.\frac{\sqrt{a^2}}{\sqrt{3b}}=3ab.\frac{\left|a\right|}{\sqrt{3b}}$

Vì a < 0 nên $\left|a\right|=-a.$ Suy ra $3ab.\frac{\left|a\right|}{\sqrt{3b}}=3ab.\frac{-a}{\sqrt{3b}}=-\frac{3a^{2}b.\sqrt{3b}}{3b}=-a^2\sqrt{3b}.$

Bài 11. Tính:

Hướng dẫn giải

a) Ta có:

b) Ta có:

c) Ta có:

Bài 12. Trục căn thức ở mẫu các biểu thức sau:

Hướng dẫn giải

a) Ta có:

b) Ta có:

c) Ta có:

Học tốt Chương 3

Các bài học để học tốt Chương 3 Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài tập cuối chương 3