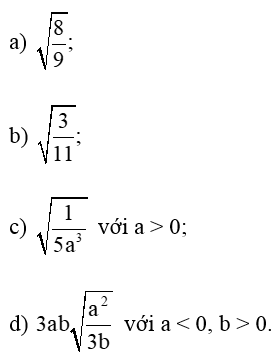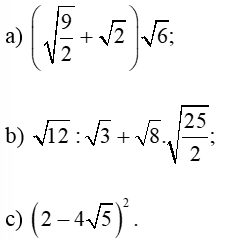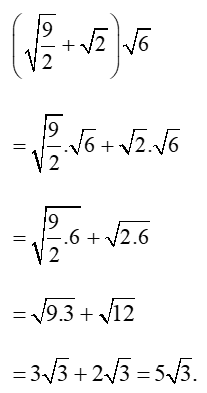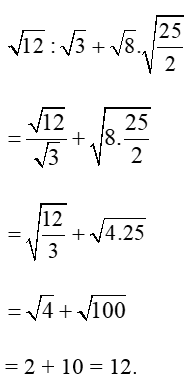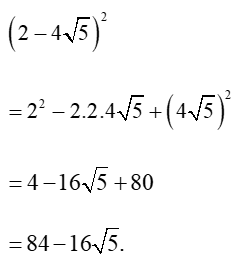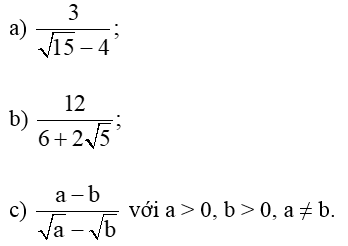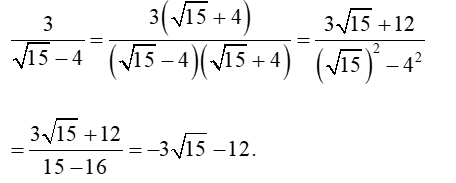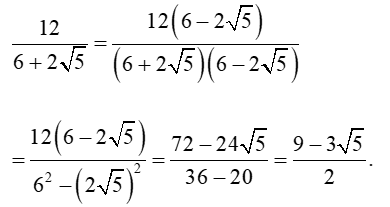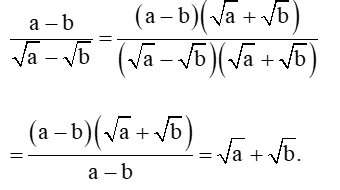Lý thuyết Toán 9 Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Biến đổi đơn giản biểu thức chứa căn thức bậc hai - Chân trời sáng tạo

Lý thuyết Biến đổi đơn giản biểu thức chứa căn thức bậc hai

1. Trục căn thức ở mẫu

• Đối với những biểu thức chứa căn thức ở mẫu, ta thường biến đổi để khử căn thức ở mẫu đó. Phép biến đổi như vậy gọi là trục căn thức ở mẫu.

• Với biểu thức $\frac{\sqrt{a}}{\sqrt{b}}$ (a ≥ 0, b > 0), ta biến đổi:

$\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{a}.\sqrt{b}}{\sqrt{b}.\sqrt{b}}=\frac{\sqrt{ab}}{b}.$

Chú ý:

• Với số thực a không âm và số thực b dương, ta thường biến đổi

$\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{a}.\sqrt{b}}{\sqrt{b}.\sqrt{b}}=\frac{\sqrt{ab}}{b}$ hoặc $\sqrt{\frac{a}{b}}=\sqrt{\frac{ab}{b^2}}=\frac{\sqrt{ab}}{\sqrt{b^2}}=\frac{\sqrt{ab}}{b}$

để khử mẫu của biểu thức dưới dấu căn.

• Tổng quát hơn, với hai biểu thức A và B thỏa mãn AB ≥ 0, B ≠ 0, ta có:

$\sqrt{\frac{A}{B}}=\sqrt{\frac{AB}{B^2}}=\frac{\sqrt{AB}}{\sqrt{B^2}}=\frac{\sqrt{AB}}{\left|B\right|}.$

Ví dụ: Trục căn thức ở mẫu các biểu thức sau:

a) $\frac{7}{\sqrt{5}-1};$

b) $\frac{3}{\sqrt{4}+\sqrt{5}}.$

Hướng dẫn giải

a) Ta có: $\frac{7}{\sqrt{5}-1}=\frac{7\left(\sqrt{5}+1\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}$

$=\frac{7\left(\sqrt{5}+1\right)}{{\left(\sqrt{5}\right)}^2-1^2}=\frac{7\left(\sqrt{5}+1\right)}{5-1}=\frac{7\sqrt{5}+7}{4}.$

b) Ta có: $\frac{3}{\sqrt{4}+\sqrt{5}}=\frac{3\left(\sqrt{4}-\sqrt{5}\right)}{\left(\sqrt{4}+\sqrt{5}\right)\left(\sqrt{4}-\sqrt{5}\right)}$

$=\frac{3\left(\sqrt{4}-\sqrt{5}\right)}{{\left(\sqrt{4}\right)}^2-{\left(\sqrt{5}\right)}^2}=\frac{3\left(\sqrt{4}-\sqrt{5}\right)}{4-5}=3\sqrt{5}-3\sqrt{4}.$

Chú ý:

• Trong câu a của ví dụ trên, để trục căn thức ở mẫu, ta nhân cả tử và mẫu với biểu thức $\sqrt{5}+1.$ Ta gọi biểu thức $\sqrt{5}-1$ và biểu thức $\sqrt{5}+1$ là hai biểu thức liên hợp với nhau.

• Với hai biểu thức A, B mà B > 0, ta có $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}.$

• Với các biểu thức A, B, C mà A ≥ 0 và A ≠ B², ta có

$\frac{C}{\sqrt{A}+B}=\frac{C\left(\sqrt{A}-B\right)}{A-B^2};$$\frac{C}{\sqrt{A}-B}=\frac{C\left(\sqrt{A}+B\right)}{A-B^2}.$

• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0 và A ≠ B, ta có

$\frac{C}{\sqrt{A}+\sqrt{B}}=\frac{C\left(\sqrt{A}-\sqrt{B}\right)}{A-B};$$\frac{C}{\sqrt{A}-\sqrt{B}}=\frac{C\left(\sqrt{A}+\sqrt{B}\right)}{A-B}.$

Ví dụ: Trục căn thức ở mẫu các biểu thức sau:

a) $\frac{\sqrt{11}}{\sqrt{5}};$

b) $-\frac{13}{4\sqrt{7}}.$

Hướng dẫn giải

a) Ta có: $\frac{\sqrt{11}}{\sqrt{5}}=\frac{\sqrt{11}.\sqrt{5}}{5}=\frac{\sqrt{55}}{5}.$

b) Ta có: $-\frac{13}{4\sqrt{7}}=-\frac{13.\sqrt{7}}{4.7}=-\frac{13\sqrt{7}}{28}.$

2. Rút gọn biểu thức chứa căn thức bậc hai

• Để rút gọn biểu thức chứa căn thức bậc hai, ta thường vận dụng thích hợp các tính chất (giao hoán, kết hợp, phân phối) của các phép tính, quy tắc về thứ tự thực hiện phép tính và các phép biến đổi đã biết.

Ví dụ: Rút gọn các biểu thức sau:

a) $\sqrt{45}-2\sqrt{5};$

b) $\sqrt{18}+\sqrt{24}-\sqrt{40}.$

Hướng dẫn giải

a) Ta có: $\sqrt{45}-2\sqrt{5}=\sqrt{3^2.5}-2\sqrt{5}$

$=3\sqrt{5}-2\sqrt{5}=\left(3-2\right)\sqrt{5}=\sqrt{5}.$

b) Ta có: $\sqrt{18}+\sqrt{24}-\sqrt{40}$

$=\sqrt{3^2.2}+\sqrt{2^2.6}-\sqrt{2^2.10}$

$=3\sqrt{2}+2\sqrt{6}-2\sqrt{10}.$

Bài tập Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài 1. Khử mẫu của biểu thức lấy căn:

Hướng dẫn giải

a) Ta có: $\sqrt{\frac{8}{9}}=\frac{\sqrt{8}}{\sqrt{9}}=\frac{2\sqrt{2}}{3}.$

b) Ta có: $\sqrt{\frac{3}{11}}=\frac{\sqrt{3}}{\sqrt{11}}=\frac{\sqrt{3}.\sqrt{11}}{11}=\frac{\sqrt{33}}{11}.$

c) Ta có: $\sqrt{\frac{1}{5a^3}}=\frac{\sqrt{1}}{\sqrt{5a^3}}=\frac{1}{\sqrt{5a.a^2}}=\frac{1}{a\sqrt{5a}}=\frac{\sqrt{5a}}{5a^2}$ với a > 0.

d) Ta có: $3ab\sqrt{\frac{a^2}{3b}}=3ab.\frac{\sqrt{a^2}}{\sqrt{3b}}=3ab.\frac{\left|a\right|}{\sqrt{3b}}$

Vì a < 0 nên $\left|a\right|=-a.$ Suy ra $3ab.\frac{\left|a\right|}{\sqrt{3b}}=3ab.\frac{-a}{\sqrt{3b}}=-\frac{3a^{2}b.\sqrt{3b}}{3b}=-a^2\sqrt{3b}.$

Bài 2. Tính:

Hướng dẫn giải

a) Ta có:

b) Ta có:

c) Ta có:

Bài 3. Trục căn thức ở mẫu các biểu thức sau:

Hướng dẫn giải

a) Ta có:

b) Ta có:

c) Ta có:

Học tốt Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Các bài học để học tốt Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 4: Biến đổi đơn giản biểu thức chứa căn thức bậc hai