Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).
Câu hỏi:
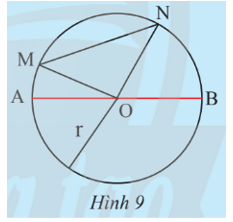
Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9).
a) Tính độ dài đoạn thẳng AB theo R.
b) So sánh độ dài của MN và OM + ON. Từ đó, so sánh độ dài của MN và AB.
Trả lời:
a) Vì hai điểm A, B cùng nằm trên đường tròn (O; R) nên OA = OB = R.
Mà AB đi qua O hay O nằm giữa A, B nên AB = OA + OB = R + R = 2R.
Vậy AB = 2R.
b) Xét ∆OMN có: OM + ON > MN (bất đẳng thức trong tam giác). (1)
Ta có hai điểm M, N cùng nằm trên đường tròn (O; R) nên OM = ON = R.
Do đó từ (1) ta có R + R > MN hay 2R > MN.
Mà AB = 2R (câu a) nên AB > MN.
Xem thêm lời giải bài tập Toán 9 Chân trời sáng tạo hay, chi tiết:
Câu 1:
Hãy chỉ ra các bộ phận có dạng đường tròn của chiếc xe đạp trong hình dưới đây. Em hãy tìm thêm một số hình ảnh về đường tròn trong thực tế.
Xem lời giải »
Câu 2:
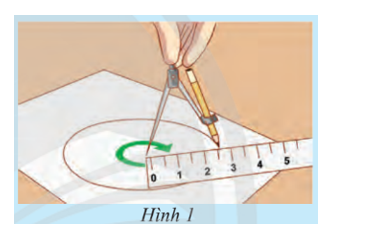
Mở một chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước. Tì đầu nhọn của compa lên một điểm O cố định trên tờ giấy, xoay compa để đầu bút M của compa vạch trên giấy một đường cong. Nêu nhận xét về các khoảng cách từ một điểm M tuỳ ý trên đường cong vừa vẽ đến điểm O.
Xem lời giải »
Câu 3:
a) Cho đường tròn (O; R).
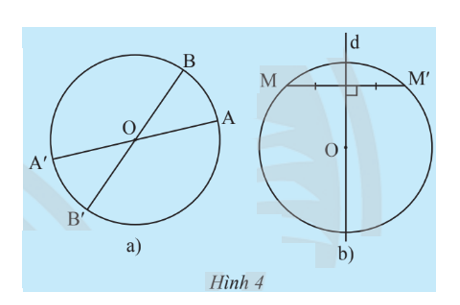
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O; R). Tìm điểm B’ sao cho O là trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O; R) không? Giải thích.
b) Cho đường tròn (O; R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O; R) không? Giải thích.
Xem lời giải »
Câu 4:
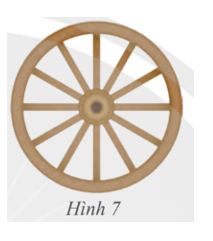
Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm.
Xem lời giải »
Câu 5:
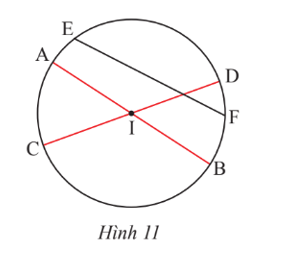
Cho đường tròn (I) có các dây cung AB, CD, EF. Cho biết AB và CD đi qua tâm I, EF không đi qua I (Hình 11). Hãy so sánh độ dài AB, CD, EF.
Xem lời giải »
Câu 6:
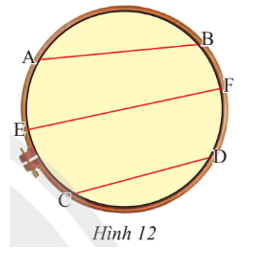
Bạn Mai căng ba đoạn chỉ AB, CD, EF có độ dài lần lượt là 16 cm, 14 cm và 20 cm trên một khung thêu hình tròn bán kính 10 cm (Hình 12). Trong ba dây trên, dây nào đi qua tâm của đường tròn? Giải thích.
Xem lời giải »
Câu 7:
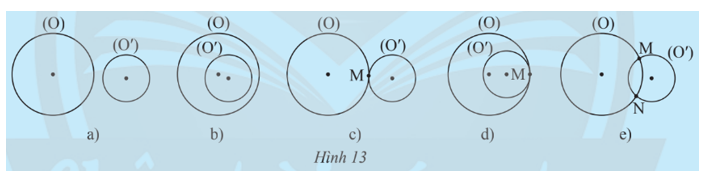
Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:
Xem lời giải »
Câu 8:
Cho hai đường tròn phân biệt (O; R) và (O’; R’) với R ≥ R’. Hãy so sánh OO’ với R + R’ và R – R’ trong mỗi trường hợp sau:
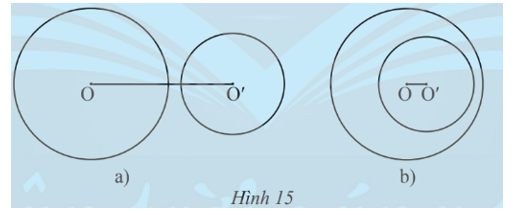
Trường hợp 1: (O; R) và (O’; R’) không có điểm chung (Hình 15).
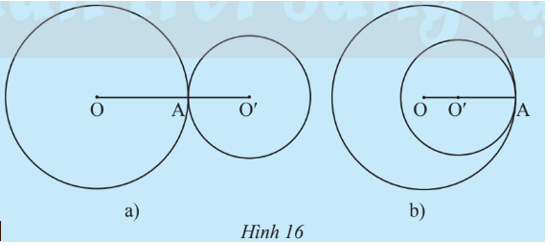
Trường hợp 2: (O; R) và (O’; R’) chỉ có một điểm chung (Hình 16).
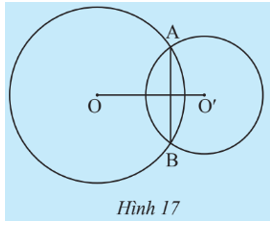
Trường hợp 3: (O; R) và (O’; R’) có đúng hai điểm chung (Hình 17).
Xem lời giải »