1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b
Câu hỏi:
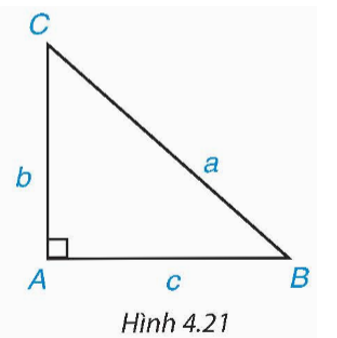
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).
Trả lời:
1. Trường hợp biết AB = c và AC = b, ta cần tính BC và các góc của tam giác.
Xét ∆ABC vuông tại A, sử dụng định nghĩa tỉ số lượng giác tan, ta có: Từ đó ta tính được góc B, khi đó ta tính được góc C thông qua định lí tổng ba góc của một tam giác.
Sau đó, sử dụng định lí 1, ta có AC = BC.sinB, suy ra
Trường hợp biết AB = c và BC = a, ta cần tính AC và các góc của tam giác.
Xét ∆ABC vuông tại A, sử dụng định nghĩa tỉ số lượng giác cos, ta có: Từ đó ta tính được góc B, khi đó ta tính được góc C thông qua định lí tổng ba góc của một tam giác.
Sau đó, sử dụng định lí 1, ta có AC = BC.sinB = a.sinB.