b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O).
Câu hỏi:
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.
Trả lời:
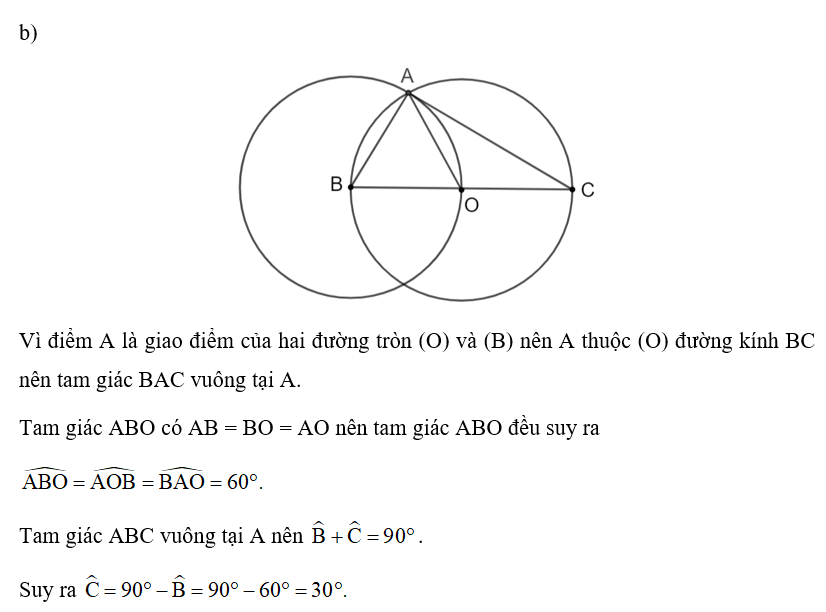
Câu hỏi:
b) Giả sử A là một trong hai giao điểm của đường tròn (B; BO) với đường tròn (O). Tính các góc của tam giác ABC.
Trả lời:

Câu 1:
Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng và OB = 4 cm. Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Câu 2:
Cho hình 5.43, trong đó BD là đường kính,
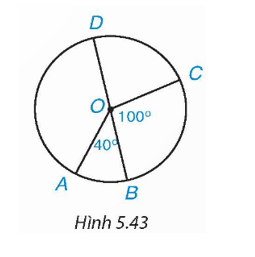
Khi đó:
A. và .
B. và .
C. và .
D. và .
Câu 3:
Cho hai đường tròn (A; R1), (B; R2), trong đó R2 < R1. Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.44).
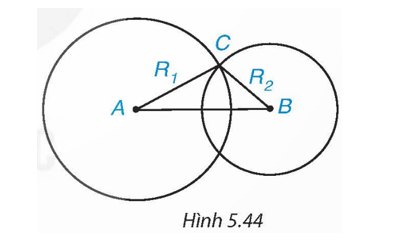
Khi đó:
A. AB < R1 − R2.
B. R1 − R2 < AB < R1 + R2.
C. AB > R1 + R2.
D. AB = R1 + R2.
Câu 4:
Cho đường tròn (O; R) và hai đường thẳng a1 và a2. Gọi d1, d2 lần lượt là khoảng cách từ điểm O đến a1 và a2. Biết rằng (O) cắt a1 và tiếp xúc với a2 (H.5.45).
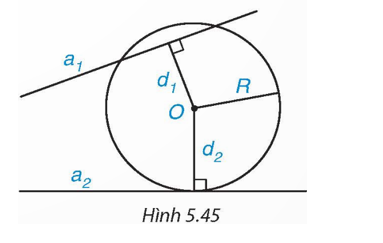
Khi đó:
A. d1 < R, d2 = R.
B. d1 = R, d2 < R.
C. d1 > R, d2 = R.
D. d1 < R, d2 < R.
Câu 5:
Câu 6:
Cho AB là một dây bất kì (không phải là đường kính) của đường tròn (O; 4 cm). Gọi C và D lần lượt là các điểm đối xứng với A và B qua tâm O.
a) Hai điểm C và D có nằm trên đường tròn (O) không? Vì sao?
Câu 7:
b) Biết rằng ABCD là một hình vuông. Tính độ dài cung lớn AB và diện tích hình quạt tròn tạo bởi hai bán kính OA và OB.
Câu 8:
Cho điểm B nằm giữa hai điểm A và C, sao cho AB = 2 cm và BC = 1 cm. Vẽ các đường tròn (A; 1,5 cm), (B; 3 cm) và (C; 2 cm). Hãy xác định các cặp đường tròn:
a) Cắt nhau;
b) Không giao nhau;
c) Tiếp xúc với nhau.
