Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng OA = căn bậc hai 15 cm và OB = 4 cm. Khi đó:
Câu hỏi:
Cho đường tròn (O; 4 cm) và hai điểm A, B. Biết rằng và OB = 4 cm. Khi đó:
A. Điểm A nằm trong (O), điểm B nằm ngoài (O).
B. Điểm A nằm ngoài (O), điểm B nằm trên (O).
C. Điểm A nằm trên (O), điểm B nằm trong (O).
D. Điểm A nằm trong (O), điểm B nằm trên (O).
Trả lời:
Đáp án đúng là: D
Vì nên điểm A nằm trong (O; 4 cm).
Vì OB = 4 cm nên điểm B nằm trên (O; 4 cm).
Vậy điểm A nằm trong (O), điểm B nằm trên (O).
Xem thêm lời giải bài tập Toán 9 Kết nối tri thức hay, chi tiết:
Câu 1:
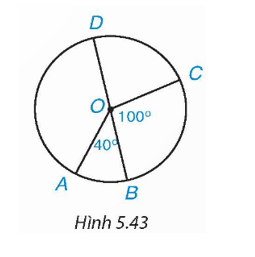
Cho hình 5.43, trong đó BD là đường kính,
Khi đó:
A. và .
B. và .
C. và .
D. và .
Xem lời giải »
Câu 2:
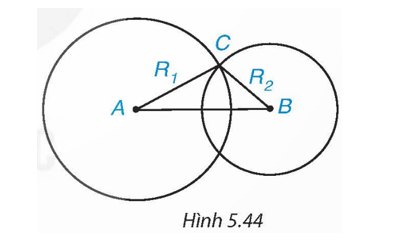
Cho hai đường tròn (A; R1), (B; R2), trong đó R2 < R1. Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.44).
Khi đó:
A. AB < R1 − R2.
B. R1 − R2 < AB < R1 + R2.
C. AB > R1 + R2.
D. AB = R1 + R2.
Xem lời giải »
Câu 3:
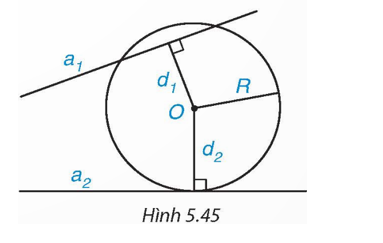
Cho đường tròn (O; R) và hai đường thẳng a1 và a2. Gọi d1, d2 lần lượt là khoảng cách từ điểm O đến a1 và a2. Biết rằng (O) cắt a1 và tiếp xúc với a2 (H.5.45).
Khi đó:
A. d1 < R, d2 = R.
B. d1 = R, d2 < R.
C. d1 > R, d2 = R.
D. d1 < R, d2 < R.
Xem lời giải »
Câu 4:
Cho đường tròn (O) đường kính BC và điểm A (khác B và C).
a) Chứng minh rằng nếu A nằm trên (O) thì ABC là một tam giác vuông; ngược lại, nếu ABC là tam giác vuông tại A thì nằm trên (O).
Xem lời giải »