Bài 5.14 trang 97 Toán 9 Kết nối tri thức Tập 1
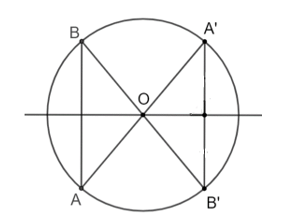
Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng với A và B qua (O). Hỏi đường trung trực của A'B' có phải là trục đối xứng của (O) hay không? Tại sao?
Giải Toán 9 Luyện tập chung - Kết nối tri thức
Bài 5.14 trang 97 Toán 9 Tập 1: Cho dây AB không qua tâm của đường tròn (O). Gọi A' và B' là hai điểm lần lượt đối xứng với A và B qua (O). Hỏi đường trung trực của A'B' có phải là trục đối xứng của (O) hay không? Tại sao?
Lời giải:
Vì A' và B' là hai điểm lần lượt đối xứng với A và B qua (O) nên OA = OA', OB = OB'.
Mà dây AB không qua tâm của đường tròn (O) nên OA = OB (đều là bán kính của đường tròn (O)).
Suy ra OA = OA' = OB = OB'.
Do đó, O thuộc đường trung trực của A'B'.
Vậy đường trung trực của A'B' là một trục đối xứng của (O).
Lời giải bài tập Toán 9 Luyện tập chung hay, chi tiết khác: