HĐ5 trang 74 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9
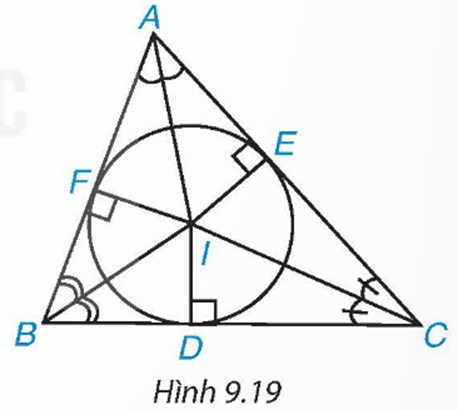
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
Giải Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác - Kết nối tri thức
HĐ5 trang 74 Toán 9 Tập 2: Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D, E, F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC, CA và AB (H.9.19).
a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.
Lời giải:
a) Vì I là giao điểm của ba đường phân giác của tam giác ABC nên I cách đều ba cạnh của tam giác đó.
Mặt khác, ID ⊥ BC, IE ⊥ CA, IF ⊥ AB nên ID = IE = IF.
Do đó các điểm D, E, F cùng nằm trên một đường tròn có tâm I.
b) Gọi (I; R) là đường tròn đi qua ba điểm D, E, F. Do đó ID = IE = IF = R.
Vì ID ⊥ BC, ID = R nên BC là tiếp tuyến của (I; R) hay (I) tiếp xúc với cạnh BC.
Vì IE ⊥ AC, IE = R nên AC là tiếp tuyến của (I; R) hay (I) tiếp xúc với cạnh AC.
Vì IF ⊥ AB, IF = R nên AB là tiếp tuyến của (I; R) hay (I) tiếp xúc với cạnh AB.
Vậy (I) tiếp xúc với các cạnh của tam giác ABC.
Lời giải bài tập Toán 9 Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác hay, chi tiết khác:
Mở đầu trang 72 Toán 9 Tập 2: Cho trước một tam giác ABC. Bằng thước kẻ và compa ....
HĐ1 trang 72 Toán 9 Tập 2: Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d ....
HĐ2 trang 72 Toán 9 Tập 2: Cho tam giác ABC có ba đường trung trực đồng quy tại O ....
Câu hỏi trang 73 Toán 9 Tập 2: Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong Hình 9.14 ....
Luyện tập 1 trang 73 Toán 9 Tập 2: Cho tam giác ABC có AC = 3 cm, AB = 4 cm và BC = 5 cm ....
Câu hỏi trang 75 Toán 9 Tập 2: Mỗi tam giác có bao nhiêu đường tròn nội tiếp? ....
HĐ6 trang 75 Toán 9 Tập 2: Cho tam giác đều ABC có trọng tâm G ....
Thực hành trang 75 Toán 9 Tập 2: Vẽ đường tròn nội tiếp của tam giác ABC bằng thước kẻ ....
Luyện tập 3 trang 76 Toán 9 Tập 2: Cho tam giác đều ABC (H.9.22) ....
Bài 9.7 trang 76 Toán 9 Tập 2: Cho đường tròn (O) ngoại tiếp tam giác ABC ....
Bài 9.8 trang 76 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) ....